Subsection 5.1.1 Work
If an object is displaced along the same direction as the force is applied then the work is said to be done. If a force \(F\) displaces a body to a distance \(d\) along the direction of force then work can be calculated by \(W= Fd\text{.}\) Work is a scalar quantity as it is a measure of transfer of energy from one object to another. The physical quantities which can be obtained by dot product of two vectors are scalar.
\begin{equation*}
\vec{A} \cdot \vec{B} = A B \cos\theta = A_{x} B_{x} + A_{y} B_{y} + A_{z} B_{z} \quad \textbf{Dot Product}
\end{equation*}
The unit of work is joule in SI system, \(Joule (J) = N.m\text{;}\) in FPS system, ft-lb = foot.pound; and in CGS system, erg = dyne.cm.
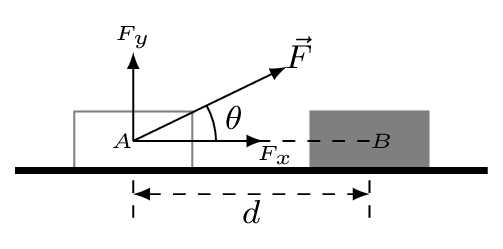
Suppose a block of mass \(m\) is displaced to a distance \(d\) along the horizontal direction by the application of force \(\vec{F}\) [Figure 5.1.1.(a)]. If the force \(\vec{F}\) is acting along a direction \(\theta\) to the horizontal, then work done by the force is given by
\begin{equation}
W=\vec{F}\cdot\vec{d}=Fd\cos\theta = (F\cos\theta)d = F_{x}d\tag{5.1.1}
\end{equation}
The work done by a force is defined as the product of component of the force in the direction of displacement and the magnitude of displacement. Work in physics is different than our daily life work. Suppose you are pushing a rigid brick wall very hard, after some time you get exhausted because you lose your body energy. In our daily life we called this action as a work, but in physics this is not a work because the object did not displace from its position. Hence in physics, whether the force or the displacement is zero, there is no work. Depending upon the angle between the applied force and the displacement, work could be negative, positive, or zero. For example, work done by a frictional force, or work done by a force acting opposite to the motion of object,
\begin{equation*}
W_{f}=\vec{f}\cdot\vec{d} = -fd,
\end{equation*}
work done by a force acting parallel to the motion of object,
\begin{equation*}
W_{F}=\vec{F}\cdot\vec{d} = Fd\cos0^{o}=Fd,
\end{equation*}
and work done by a force acting perpendicular to the motion of object,
\begin{equation*}
W_{F}=\vec{F}\cdot\vec{d} = Fd\cos90^{o}=0.
\end{equation*}
If a force
\begin{equation*}
\vec{F}=F_{x} \hat{i}+ F_{y} \hat{j}+F_{z} \hat{k}
\end{equation*}
displaces an object to a small distance \(\,d\vec{r},\) where
\begin{equation*}
\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}
\end{equation*}
then work done by this force is given by
1
If
\begin{equation*}
\vec{r}=x\hat{i}+y\hat{j}+z\hat{k},
\end{equation*}
then
\begin{equation*}
\,dr = \,dx\hat{i}+\,dy\hat{j}+\,dz\hat{k}
\end{equation*}
\begin{equation*}
W=\int \vec{F}\cdot\,d\vec{r} = \int F\cos\theta\,dr = \int F_{x}\,dx+\int F_{y}\,dy+\int F_{z}\,dz
\end{equation*}
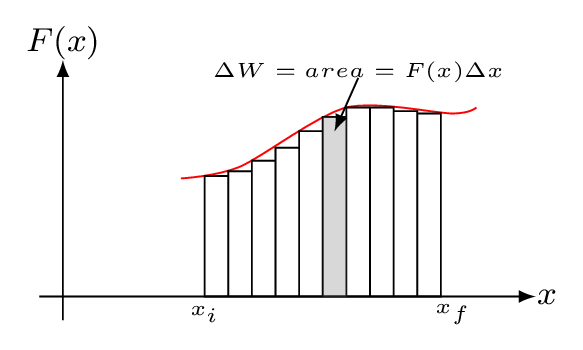
The terms like \(F_{x}\,dx\) are area under the curve [Figure 5.1.1.(b)]. The sum of these area between initial position to final position along each direction is equal to work done by a variable force F(r), such as force of spring.
