Subsection 9.1.1 Pascal’s Principle
Pascal’s principle states that pressure applied to an enclosed fluid is transmitted equally to every portion of the fluid and the walls of the container. This principle is valid only for an incompressible fluid which is most of the liquid. Hydraulic press is one of the good examples of Pascal’s principle. It is a device to lift heavy objects. It has two cylindrical opening attached the horizontal tube as shown in Figure 9.1.1. An incompressible liquid is filled in the device. It works on Pascal’s principle and obeys the conservation of energy. Work done on the a pump (small cylindrical piston) to push it down is equal to the work done by the big piston to lift heavy objects like vehicle, elephant, etc. Let a force \(F_{1}\) is applied on one piston to push it to a distance \(\,dx_{1} \) then it lifts the weight \(F_{2}\) to a distance \(\,dx_{2}\) on the other pan attached to the second piston.
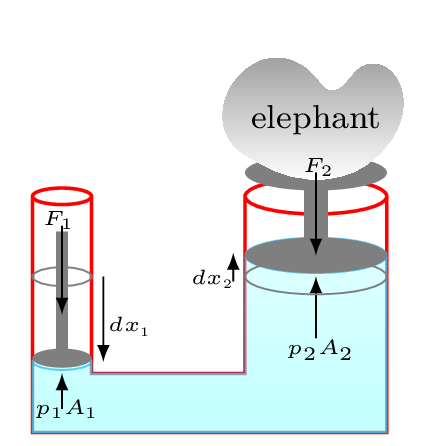
\begin{equation*}
\therefore \quad \,dW_{1} = \,dW_{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad F_{1}\,dx_{1} =F_{2}\,dx_{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad p_{1}A_{1}\,dx_{1} =p_{2}A_{2}\,dx_{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad p_{1}\,dV_{1} =p_{2}\,dV_{2}
\end{equation*}
Since the hydraulic fluid is incompressible \(\,dV_{1}=\,dV_{2}.\)
\begin{equation}
\therefore \quad p_{1}=p_{2} \tag{9.1.1}
\end{equation}
which is the Pascal’s principle. Also
\begin{equation*}
\frac{F_{1}}{A_{1}}=\frac{F_{2}}{A_{2}}
\end{equation*}
\begin{equation}
\Rightarrow \quad F_{2} = \frac{A_{2}}{A_{1}}F_{1} \tag{9.1.2}
\end{equation}
Since area of cross-section,\(A_{2}\) is greater than area of cross-section, \(A_{1}\) a small force \(F_{1}\) can generate a compressive force \(F_{2}.\)
Subsubsection 9.1.1.1 Measurement of Fluid Pressure
Pressure measurement is important in many occasions in our daily life. To check tire pressure, pressure in balloon filled with air, pressure inside a pipe carrying fluid, pressure in gas cylinder, pressure in boiler used in industries, and pressure inside an airplane cabin. Two basic types of pressure measuring devices have been discussed here.
-
Manometer: Manometer is is a U-shaped tube used to measure pressure of a fluid at rest. It contains water, mercury, or any other suitable fluid in the tube. When a pressure line is connected to one column of manometer, the fluid in the column will be forced down, and the fluid in the other will rise as shown in Figure 9.1.2. By measuring the difference in height of the fluid in the two columns, the pressure of the inlet can be expressed in length.
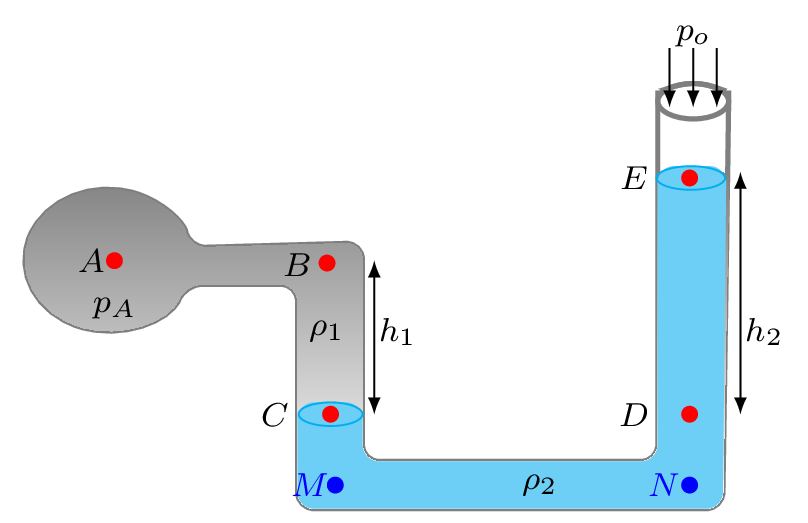
Figure 9.1.2. \begin{equation*} p_{C} =p_{B}+\rho_{1}gh_{1} \end{equation*}\begin{equation*} p_{C} =p_{A}+\rho_{1}gh_{1} =p_{D} \end{equation*}\begin{equation*} p_{D} =p_{o}+\rho_{2}gh_{2} \end{equation*}\begin{equation*} p_{A}+\rho_{1}gh_{1} =p_{o}+\rho_{2}gh_{2} \end{equation*}\begin{equation*} \therefore\quad p_{A,abs} = p_{o} +\rho_{2}gh_{2} -\rho_{1}gh_{1} \end{equation*}\begin{equation*} \therefore\quad p_{A,gauge} = \rho_{2}gh_{2} -\rho_{1}gh_{1} \end{equation*}Here \(p_{o}\) is an atmospheric pressure acting on the open end of manometer, \(\rho_{1}\) and \(\rho_{2} \) are densities of fluids in container A and in U-tube, respectively. Pressure at points A and B are same and the pressure at points C and D are same. Hence pressure in column BC is balanced by pressure in column DE.alternate:\begin{equation*} p_{M} = p_{N} \end{equation*}\begin{equation*} \text{or,} \quad p_{A}+\rho_{1}gh_{1} = p_{o}+\rho_{2}g h_{2} \end{equation*}\begin{equation*} \therefore\quad p_{A}-p_{o} = \rho_{2}gh_{2}-\rho_{1}gh_{1} =p_{A,gauge} \end{equation*} -
Barometer It is the simplest pressure gauge used for measuring atmospheric pressure. It is designed by Torricelli. A meter long tube completely filled with mercury is inverted in a mercury container in such a way that the open end of the tube is under the pool of mercury. Now on balancing the atmospheric pressure acting on the mercury container the mercury column in the tube drops to a certain height and creating a complete vacuum at the top of the tube and hence the pressure is zero at point C. In the Figure 9.1.3, points A and B are at the same level so they have the same pressure.
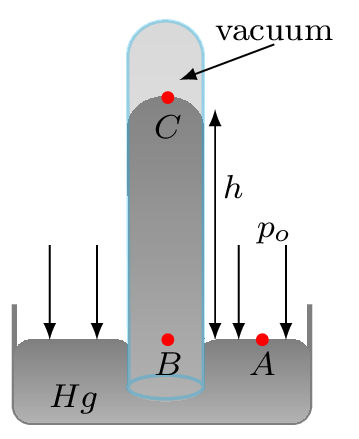
Figure 9.1.3. \begin{equation*} p_{A}=p_{B} = h\rho g = p_{o} \end{equation*}This device measures atmospheric pressure, rather than gauge pressure, because there is a nearly pure vacuum above the mercury in the tube.
