Subsection 3.3.3 Motion in Polar Coordinates
In polar coordinates, the position of a particle P, is determined by the position vector, \(\vec{r},\) and the angle \(\theta\) of the vector with the horizontal axis. The trajectory of the particle is given by a function of \(r(t),\theta(t)\text{.}\)
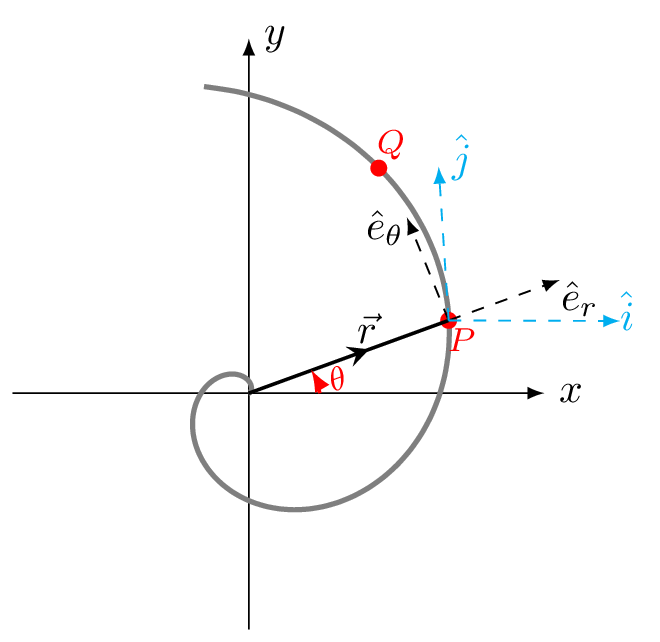
From Figure 3.3.5,
\begin{equation*}
\hat{e}_{r}=\cos\theta\hat{i}+\sin\theta\hat{j}
\end{equation*}
\begin{equation*}
\text{and} \quad \hat{e}_{\theta}=-\sin\theta\hat{i}+\cos\theta\hat{j}
\end{equation*}
where \(\hat{e}_{r}\) and \(\hat{e}_{\theta}\) are unit vectors at point P along radial and circumferential directions and are perpendicular to each other. Now,
\begin{equation*}
\vec{r}=x\hat{i}+y\hat{j} = r\cos\theta\hat{i}+r\sin\theta\hat{j} = r\left(\cos\theta\hat{i}+\sin\theta\hat{j}\right) =r\hat{e}_{r}
\end{equation*}
\begin{equation*}
\frac{\,d\hat{e}_{r}}{\,dr} =0, \qquad \frac{\,d\hat{e}_{\theta}}{\,dr} =0
\end{equation*}
\begin{equation*}
\frac{\,d\hat{e}_{r}}{\,d\theta} =-\sin\theta\hat{i}+\cos\theta\hat{j} = \hat{e}_{\theta},
\end{equation*}
\begin{equation*}
\text{and} \quad \frac{\,d\hat{e}_{\theta}}{\,d\theta} =-\cos\theta\hat{i}-\sin\theta\hat{j} = -\hat{e}_{r}
\end{equation*}
\begin{equation*}
\therefore v= \dot{\vec{r}} = \dot{r} \hat{e}_{r} +r\dot{\theta}\hat{e}_{\theta} =v_{r}\hat{e}_{r}+v_{\theta} \hat{e}_{\theta}
\end{equation*}
\begin{equation*}
Hence, \quad v_{r}= \dot{r} \quad \text{and}\quad v_{\theta}=r\dot{\theta}
\end{equation*}
Where \(v_{r}\text{,}\) and \(v_{\theta}\) are radial and circumferential component of velocity, respectively. The radial velocity describe the rate at which \(r\) stretches and circumferential velocity describe the rate at which \(r\) swings. Now,
\begin{equation*}
\vec{a} = \dot{\vec{v}} = \ddot{r}\hat{e}_{r}+\dot{r}\hat{\dot{e}}_{r} +\dot{r}\dot{\theta}\hat{e}_{\theta}+r\ddot{\theta} \hat{e}_{\theta}+ r\dot{\theta}\hat{\dot{e}}_{\theta}
\end{equation*}
\begin{equation*}
\because \quad \hat{\dot{e}}_{r} = -\sin\theta\dot{\theta}\hat{i}+\cos\theta\dot{\theta}\hat{j} =\dot{\theta}\hat{e}_{\theta}
\end{equation*}
\begin{equation*}
also, \quad \hat{\dot{e}}_{\theta} = -\cos\theta\dot{\theta}\hat{i}-\sin\theta\dot{\theta}\hat{j}
=-\dot{\theta}\hat{e}_{r}
\end{equation*}
\begin{equation*}
\therefore \vec{a} = \left(\ddot{r} -r\dot{\theta}^{2}\right)\hat{e}_{r} +\left(r\ddot{\theta}+2\dot{r}\dot{\theta}\right)\hat{e}_{\theta} =a_{r}+a_{\theta}
\end{equation*}
\begin{equation*}
\therefore a_{r} = \left(\ddot{r} -r\dot{\theta}^{2}\right)
\end{equation*}
\begin{equation*}
\text{and}\quad a_{\theta} = \left(r\ddot{\theta}+2\dot{r}\dot{\theta}\right)
\end{equation*}
