Subsection 10.6.9 Carnot’s Theorem:
The efficiency of all reversible engines operating between the same two temperatures is the same, and no irreversible engine operating between these temperatures can be more efficient than a reversible engine working between the same two temperatures.
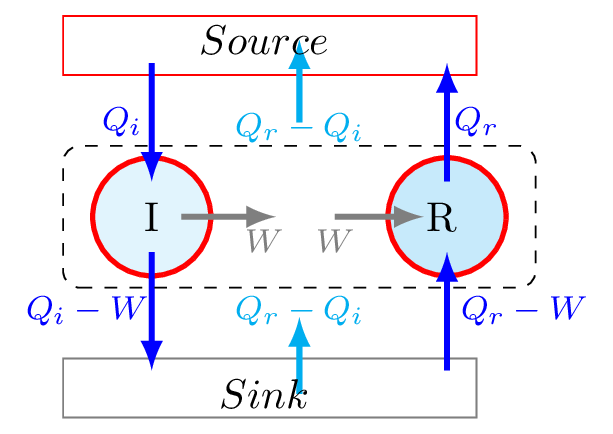
Consider two engines I and R working between the same two temperatures where I is irreversible and R is reversible. The two engines are so designed that they perform equal amount of work. If engine R draws \(Q_{r}\) amount of heat from source does W work done and rejects \(Q_{r}-W\) amount of heat to the sink then its efficiency,
\begin{equation*}
\eta_{r}= \frac{W}{Q_{r}}
\end{equation*}
Similarly, if the engine I extracts \(Q_{i}\) amount of heat from the source, perform the same amount of work W, and rejects the \(Q_{i}-W\) to the sink, then its efficiency,
\begin{equation*}
\eta_{i} = \frac{W}{Q_{i}}
\end{equation*}
Now, assume that the irreversible engine I is more efficient than the reversible engine R, then we have
\begin{equation*}
\eta_{i} \gt \eta_{r}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{W}{Q_{i}} \gt \frac{W}{Q_{r}}
\end{equation*}
\begin{equation*}
\text{or,}\quad Q_{r} \gt Q_{i}
\end{equation*}
That is, \(Q_{r} - Q_{i}\) is a positive quantity.
Now combine these two engines in such a way that engine I drives the engine R in the backward direction, so that R behaves as a refrigerator. The refrigerator R then extracts \(Q_{r}-W\) heat from the sink, after \(W\) work done on it by I it rejects \(Q_{r} \) heat to the source. The two engines are so coupled that they behave as a self acting machine. Since the work needed to run the refrigerator R is supplied by the irreversible engine I. The quantity of heat extracted from the sink is given by
\begin{equation*}
(Q_{r}-W)-(Q_{i}-W)= Q_{r}-Q_{i} = +ve
\end{equation*}
This is also the net amount of heat rejected to the source.That is this device transfers the same amount of heat \(Q_{r}-Q_{i} \) from the sink to the source without the aid of any external source. This violates the second law of thermodynamics. Hence an irreversible engine never be more efficient than the reversible one.
Now consider the reversible engines \(R_{1}\) and \(R_{2}\) are working between the same source and sink. Let \(R_{1}\) be driving backward, then as described above, \(R_{1}\) can not be more efficient than \(R_{2}\text{.}\) Similarly if \(R_{2}\) is driving \(R_{1}\) backward, then \(R_{2}\) can not be more efficient than \(R_{1}\text{.}\) Hence the two engines must have same efficiency.
