Subsection 7.1.7 Moment of Inertia of a Cylinder
Subsubsection 7.1.7.1 Moment of inertia of a thin hollow cylinder about an axis passing through its center of mass and perpendicular to its plane
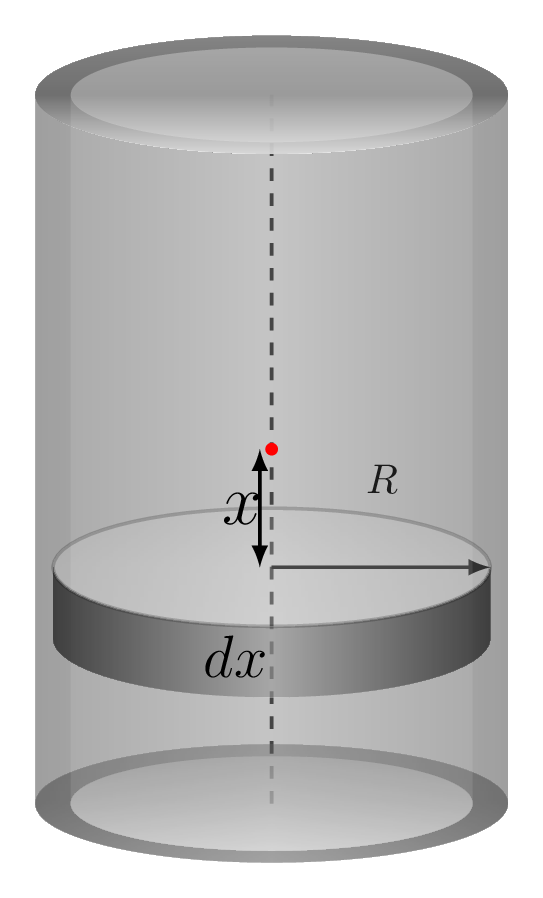
Consider an elemental ring of thickness \(\,dx\) at a distance \(x\) from the center of mass of a hollow cylinder [Figure 7.1.10.(a)], then the moment of inertia of this ring is given by
\begin{equation*}
\,dI=\,dm\,R^{2}
\end{equation*}
\begin{equation*}
\therefore\quad I = \int\limits_{0}^{l}\left(\frac{M}{2\pi Rl}\right)(2\pi R \,dx)R^{2}=\frac{MR^{2}}{l}\left(l\right)_{0}^{l}=MR^{2}
\end{equation*}
[Mass of an elemental ring = (mass per unit area of a cylinder) (area of a ring).] Here \(M\) is mass of the cylinder, \(R\) is its radius, and \(l\) is its length.
Subsubsection 7.1.7.2 Moment of inertia of a thick hollow cylinder about an axis passing through its center of mass and perpendicular to its plane
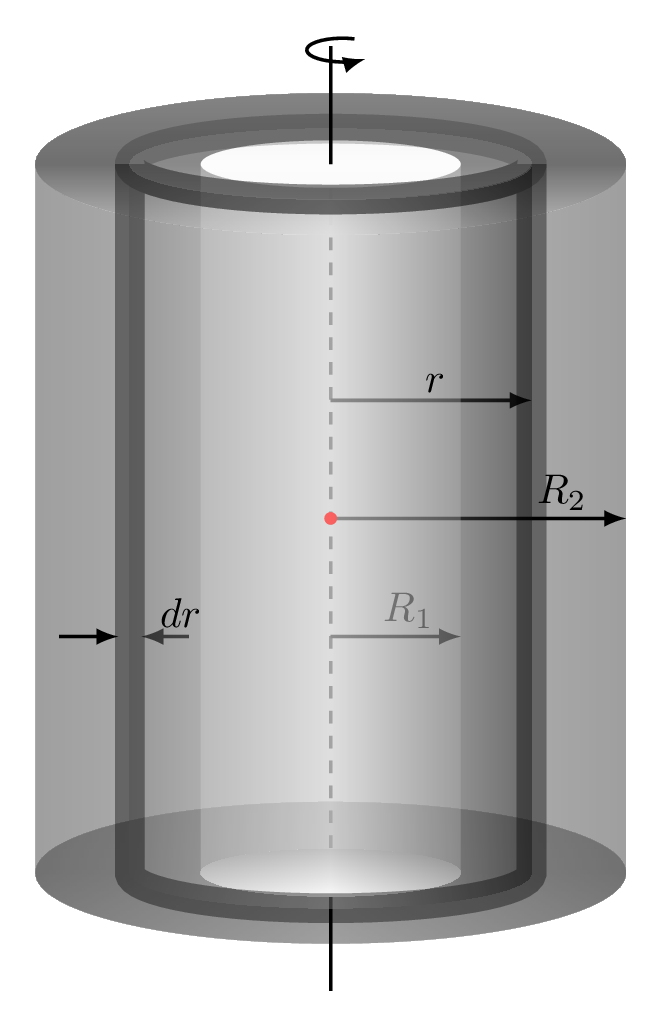
Consider an elemental thin cylinder of length \(l\text{,}\) thickness \(\,dr\) at a distance \(r\) from the center of mass of a thick hollow cylinder of outer radius \(R_{2}\) and inner radius \(R_{1}\) [Figure 7.1.10.(b)], then the moment of inertia of this cylinder is given by
\begin{equation*}
\,dI=\,dm\,r^{2} = \left[\frac{M}{\pi\left(R^{2}_{2}-R^{2}_{1}\right)l}\right]\left(2\pi r\,dr l\right)r^{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad I = \left(\frac{2M}{R_{2}^{2}-R_{1}^{2}}\right) \int\limits_{R_{1}}^{R_{2}}r^{3}\,dr
\end{equation*}
\begin{equation*}
=\left(\frac{2M}{R_{2}^{2}-R_{1}^{2}}\right)\left(\frac{r^{4}}{4}\right)_{R_{1}}^{R_{2}}
\end{equation*}
\begin{equation*}
\therefore\quad I = \frac{1}{2}\left(\frac{M}{R_{2}^{2}-R_{1}^{2}}\right)\left(R_{2}^{4}-R_{1}^{4}\right)
\end{equation*}
\begin{equation*}
= \frac{1}{2}M\left(R_{2}^{2}+R_{1}^{2}\right)
\end{equation*}
[Mass of an elemental cylinder = (mass per unit volume of a thick cylinder) (volume of elemental cylinder).]
Subsubsection 7.1.7.3 Moment of inertia of a solid cylinder about an axis passing through its center of mass and perpendicular to its plane
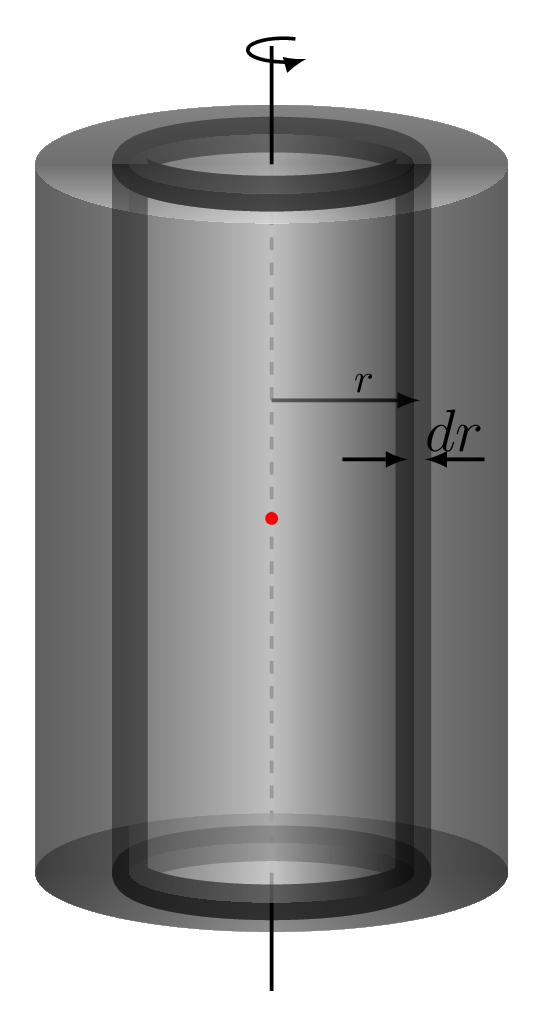
Consider a concentric cylindrical shell of length \(l\text{,}\) radius \(r\text{,}\) and thickness \(\,dr\) in a solid cylinder of mass \(M\) and radius \(R\) [Figure 7.1.10.(c)], then the moment of inertia of the shell is given by
\begin{equation*}
\,dI_{z}=\,dm\,r^{2} = \left[\frac{M}{\pi R^{2}l}\right]\left(2\pi r\,dr l\right)r^{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad I_{z} = \frac{2M}{R^{2}} \int\limits_{0}^{R}r^{3}\,dr
\end{equation*}
\begin{equation*}
=\frac{2M}{R^{2}}\left(\frac{r^{4}}{4}\right)_{0}^{R}
\end{equation*}
\begin{equation*}
\therefore\quad I_{z} = \frac{1}{2}\left(\frac{M}{R^{2}}\right)\left(R^{4}-0\right) = \frac{1}{2}MR^{2}
\end{equation*}
Show that moment of inertia of a solid cylinder about
\begin{equation*}
I_{x} =I_{y} = \frac{M}{12}\left(3R^{2}+l^{2}\right).
\end{equation*}
