Subsection 5.1.4 Principle of Conservation of Energy
It states that in an isolated system, the total energy of the system is conserved. That is, energy can neither be created nor be destroyed, it can only be converted from one form of energy to another. For example, when a block slides down a slope, potential energy is converted into kinetic energy. When friction slows the block to a stop, the kinetic energy is converted into thermal energy. In case of mechanical energy the sum of kinetic energy and potential energy is conserved.
For an interacting system,
\begin{equation*}
E_{f} = E_{i} + W_{ext}
\end{equation*}
and for an isolated system,
\begin{equation*}
E_{f} = E_{i}\text{.}
\end{equation*}
Mechanical energy is due to the position and motion of the object. Therefore,
\begin{equation*}
E=KE+PE=\frac{1}{2}mv^{2}+mgh
\end{equation*}
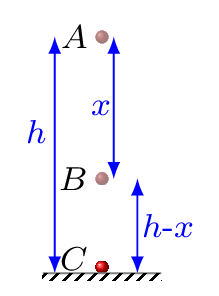
Consider a body of mass \(m\) is falling from rest at height \(h\) to the ground. We are interested in its total energy at points A, B, and C as shown in Figure 5.1.3. From the principle of conservation of energy, total energy at any point always remains same, i.e.,
\begin{equation*}
E_{A}=E_{B}=E_{C}
\end{equation*}
Where
\begin{equation*}
E_{A} = \frac{1}{2}mv_{A}^{2}+mgh= mgh \quad [\because v_{A}=0 \quad\text{at point A}]
\end{equation*}
When the body reaches to point B, then \(KE_{B} = \frac{1}{2}mv_{B}^{2},\) and \(PE_{B}=mg(h-x).\)
\begin{equation*}
\therefore E_{B} = \frac{1}{2}mv_{B}^{2}+mg(h-x)
\end{equation*}
Using equation of motion in 1D,
\begin{equation*}
v_{f}^{2}=v_{i}^{2} +2gy
\end{equation*}
\begin{equation*}
\text{or,}\quad v_{B}^{2}=0+2g(x)=2gx
\end{equation*}
\begin{equation*}
\therefore\quad E_{B} = \frac{1}{2}m(2gx)+mg(h-x) =mgx+mgh-mgx= mgh=E_{A}
\end{equation*}
Similarly,
\begin{equation*}
E_{C} = \frac{1}{2}mv_{C}^{2}+0 =\frac{1}{2}mv_{C}^{2} = \frac{1}{2}m(2gh) = mgh=E_{A}=E_{B}
\end{equation*}
\([\because v_{C}^{2}=0+2g(h)=2gh].\) Which proofs that the mechanical energy remains conserved at each and every point of the motion of an object.
