Example 4.4.1.
A 10-kg block of wood rests on the top of a 20-kg block which rests on a horizontal surface. The lower block is then pulled to the right at constant speed by a horizontal force while the top block is held at rest by a horizontal string attached to it. If the coefficient of kinetic friction for bottom surfaces and coefficient of static friction between top surfaces are 0.25.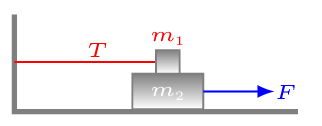 
- what is the tension in the string, and
- the force pulling the bottom block?
Solution.
Given: \(m_{1} =10 kg, \quad m_{2} =20 kg,\) and \(\mu =0.25\text{.}\)
From figure,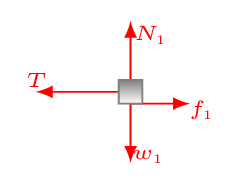 
in static equilibrium
\begin{equation*}
\sum F_{x1} = f_{1}-T =0;\qquad \sum F_{y1} = N_{1}-w_{1} =0
\end{equation*}
\begin{equation*}
w_{1} = m_{1}g; \qquad f_{1} = \mu N_{1}
\end{equation*}
From figure,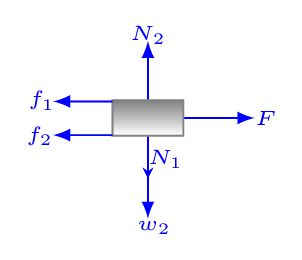 
in translational equilibrium along x-axis,
\begin{equation*}
\sum F_{x2} = F-f_{1}-f_{2} =0
\end{equation*}
in static equilibrium along y-axis,
\begin{equation*}
\sum F_{y2} = N_{2}-N_{1}-w_{2} =0
\end{equation*}
and
\begin{equation*}
w_{2} = m_{2}g; \qquad f_{2} = \mu N_{2}
\end{equation*}
Solving all these equations, we have -
\begin{equation*}
w_{1} = m_{1}g = 98N;
\end{equation*}
\begin{equation*}
N_{1} =w_{1} =98N;
\end{equation*}
\begin{equation*}
f_{1} = \mu N_{1} = 24.5N;
\end{equation*}
- \begin{equation*} \therefore \quad T = f_{1}= 24.5N \end{equation*}\begin{equation*} w_{2} = m_{2}g = 196N; \end{equation*}\begin{equation*} N_{2} =N_{1}+w_{2} =294N; \end{equation*}\begin{equation*} f_{2} = \mu N_{2} = 73.5N \end{equation*}
- \begin{equation*} \therefore\quad F = f_{1}+f_{2} = 98N \end{equation*}
