Subsection 9.5.3 Soap Bubble
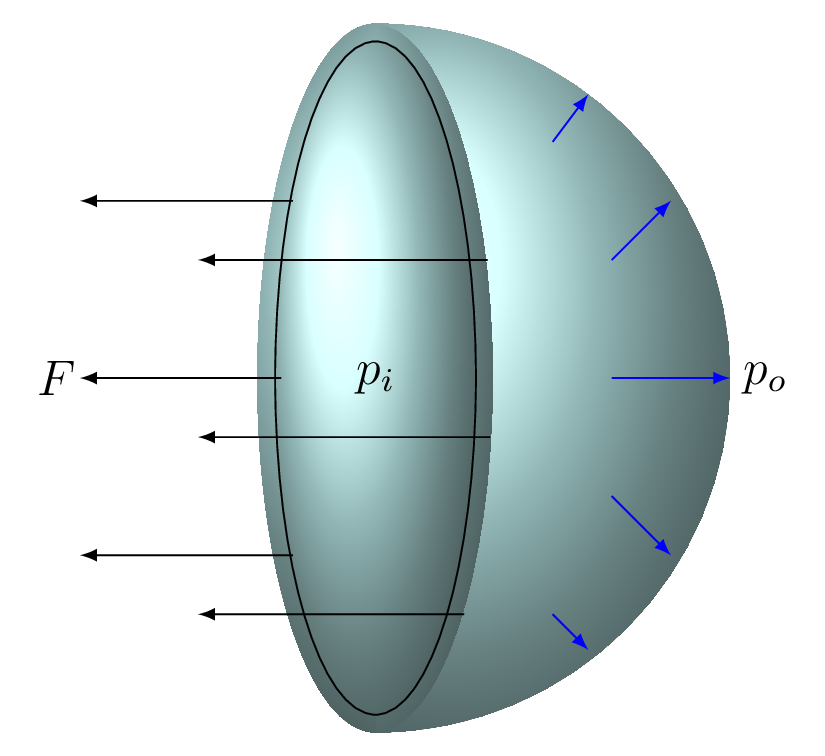
When the bubble is blown, the surface film tends to contract. This causes pressure inside the bubble to increase. The surface tension balances the outward force due to the pressure difference between the inside and the outside air. For the bubble to be stable and not collapse, the pressure inside the bubble must be higher than the pressure on the outside. In fact, there are two liquid-gas interfaces on a soap bubble, the one on the inside of the bubble and the one on the outside of the bubble Figure 9.5.5. In between the two surfaces is a thin film of liquid. The spherical shape of a soap bubble is caused by the minimization of the surface area. For a given volume, a sphere always acquires the least surface area.
The force from surface tension is \(F = 2\gamma l,\) where the factor 2 is taken because of two surfaces of the soap bubble.
\begin{equation*}
\therefore F = 2\gamma 2\pi r = 4\gamma \pi r
\end{equation*}
The force do to the pressure difference must balance the force from the surface tension. The force to the pressure difference is
\begin{equation*}
F = pA= (p_{i} - p_{o})(\pi r^{2})
\end{equation*}
\begin{equation*}
\text{or,}\quad 4\gamma \pi r = (p_{i} - p_{o})(\pi r^{2})
\end{equation*}
\begin{equation*}
\therefore\quad (\Delta p) = \frac{4\gamma}{r}
\end{equation*}
