Subsection 9.1.2 Archimedes’ Principle
When an object is placed in a fluid it experiences an upthrust force called a buoyant force. It is arising due to changes of the pressure inside fluid. This phenomenon is known as Archimedes’ principle. It states that when a body is fully or partially immersed in a fluid, the fluid exerts an upward force on the body equal to the weight of liquid displaced. That is, buoyant force (B) = weight of displaced fluid.
\begin{equation*}
B = w_{df}
\end{equation*}
Liquid does not distinguish between the volume of its own or the volume of some thing else. Meaning if we replace some arbitrary volume of the liquid with some other object of the same volume then the liquid applies the same force on its surface, Figure 9.1.4.(a) and Figure 9.1.4.(b).
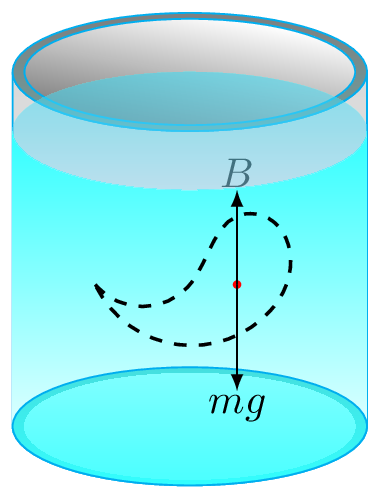
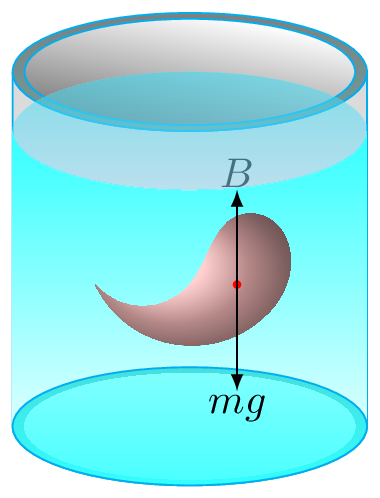
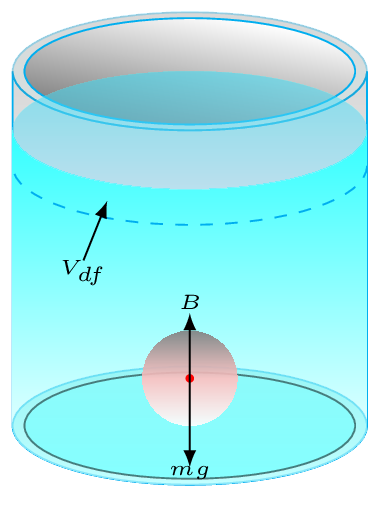
If \(m_{df}\) and \(V_{df}\) are the mass and volume of displaced fluid and \(\rho_{f} \) is the density of fluid then weight of displaced fluid is given by
\begin{equation*}
m_{df}g = V_{df}\rho_{f} g =B
\end{equation*}
Due to buoyant force body appear lighter than it really is. Hence, the weight of a body in the fluid is called an apparent weight. Weight loss of a body is equal to weight of liquid displaced. That is,
\begin{equation*}
B= W_{a}-W_{f}=\text{apparent loss in weight}
\end{equation*}
Where \(W_{a}\) and \(W_{f}\) are weight of a body in air and in the fluid, respectively. Apparent weight is the net downward force.
Hence apparent loss in weight = buoyant force = weight of water displaced.
If an object floats, then its apparent weight is zero. If its apparent weight is more than zero, it sinks. A floating object loss all of its weight.
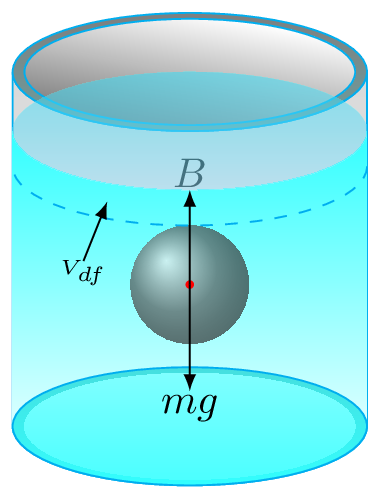
- If the body is completely submerged but suspended in the fluid [Figure 9.1.4.(c)], then from Newton’s second law net force acting on the body is zero. That is, buoyant force is equal to weight of the body\begin{equation*} B=m_{b}g \end{equation*}\begin{equation*} \text{or,}\quad V_{df}\rho_{f} g = V_{b}\rho_{b} g \end{equation*}Since body is completely immersed in the fluid, \(V_{b}=V_{df}\text{.}\) Hence,\begin{equation*} \text{or,}\quad V_{b}\rho_{f} g = V_{b}\rho_{b} g \end{equation*}\begin{equation*} \therefore \quad \rho_{f} = \rho_{b} \end{equation*}The body will suspend in a fluid if their densities are same.
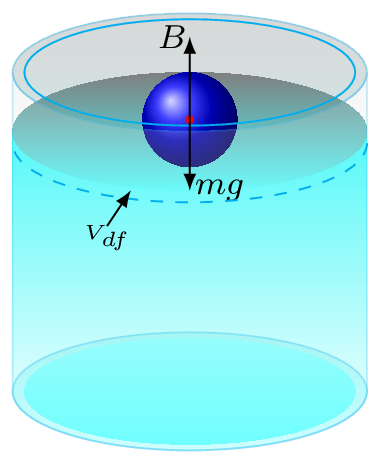
- If the body is floating in the fluid [Figure 9.1.4.(d)], then buoyant force is greater than the weight of the body. Hence body comes to a float, but at the surface of the fluid, net force acting on the body is zero.\begin{equation*} B=m_{b}g \end{equation*}\begin{equation*} \text{or,}\quad V_{df}\rho_{f} g = V_{b}\rho_{b} g \end{equation*}Since body is floating in the fluid, volume of the displaced fluid is then only equal to immersed portion of the body. Hence \(V_{df} \lt V_{b}.\)\begin{equation*} \text{or,}\quad \frac{\rho_{f}}{\rho_{b}} = \frac{V_{b}}{V_{df}} \gt 1 \end{equation*}\begin{equation*} \therefore \quad \rho_{f} \gt \rho_{b} \end{equation*}The body will float in a fluid if the densities of fluid is greater than that of the body.
- If the body is sinking in the fluid [Figure 9.1.4.(e)], then buoyant force is less than the weight of the body. Hence body sinks, but at the bottom of the fluid, net force acting on the body is zero.\begin{equation*} B+N=mg \end{equation*}\begin{equation*} \text{or,}\quad N= mg-B = V_{b}\rho_{b}g-V_{df}\rho_{f}g = V_{b}[\rho_{b}-\rho_{f}]g \end{equation*}Since \(V_{b}=V_{df}.\) Hence for \(N\) to be +ve, \(\rho_{b}-\rho_{f}\) must be positive. Here \(N\) is the apparent weight of the body in the fluid.\begin{equation*} \therefore\quad \rho_{f} \lt \rho_{b} \end{equation*}
