Subsection 9.2.2 Bernoulli’s Principle
It explains the movement of fluid through a pressure difference. work done by external force is equal to change in total energy of the fluid. If \(E_{1}\) and \(E_{2}\) are energy of the fluid at the ends of the tube where external forces \(F_{1} \) and \(F_{2},\) are acting normally on the cross-section of the tube, then
\begin{equation*}
E_{2}-E_{1} = \text{work done by external forces}
\end{equation*}
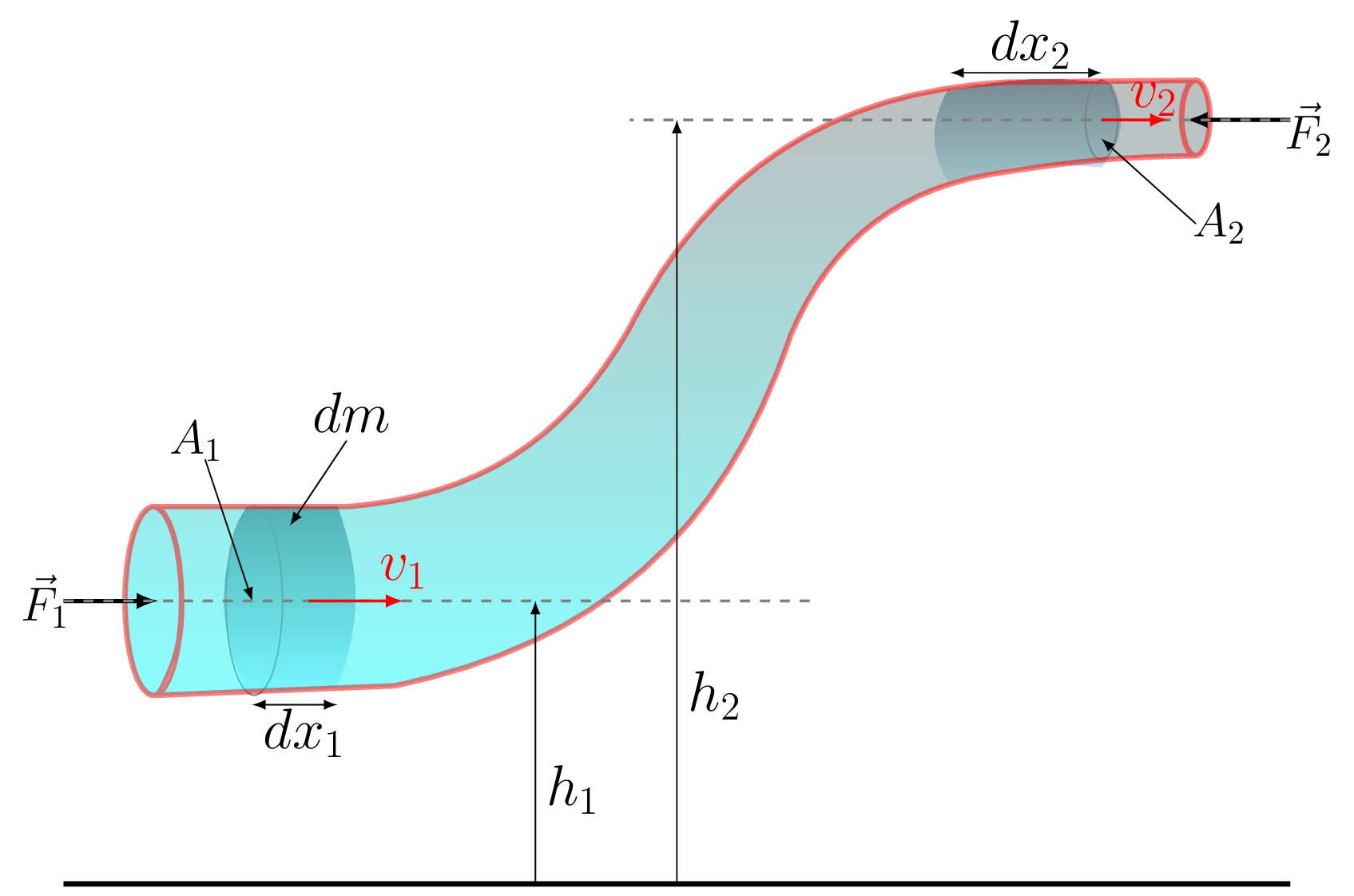
Consider a fluid is moving in a tube as shown in Figure 9.2.2. Let fluid is entering into the tube with velocity \(v_{1}\) and coming out of the tube with velocity \(v_{2}.\) The \(h_{1}\) and \(h_{2}\) are the heights of tube at its ends, respectively and \(\,dm \) is the mass of fluid flowing through the tube in time \(\,dt.\) Now,
\begin{equation*}
\left(\frac{1}{2}\,dm v^{2}_{2}+\,dm g h_{2}\right)-\left(\frac{1}{2}\,dm v^{2}_{1}+\,dm g h_{1}\right) = F_{1}\,dx_{1}- F_{2}\,dx_{2}
\end{equation*}
Here \(\,dx_{1} \) and \(\,dx_{2} \) are the distances of the fluid moves in time \(\,dt \) at its ends. Hence,
\begin{equation*}
\frac{1}{2}\,dV\rho \left(v^{2}_{2}-v^{2}_{1}\right) +\,dV\rho g \left(h_{2}-h_{1}\right) = P_{1}A_{1}\,dx_{1}- P_{2}A_{2}\,dx_{2}=\left(P_{1}-P_{2}\right)\,dV
\end{equation*}
\begin{equation*}
\therefore p_{1} + \rho gh_{1} + \frac{1}{2}\rho v_{1}^{2} = p_{2} + \rho gh_{2} + \frac{1}{2}\rho v_{2}^{2} = constant
\end{equation*}
This equation tells us that as the velocity of fluid flow increases, its pressure decreases. This is the conservation of energy principle in fluid motion. Bernoulli’s equation says that the sum of the pressure, \(P\text{,}\) (or, the energy per unit volume), the kinetic energy per unit volume ( \(\frac{1}{2}\rho v^{2}\) ), and the gravitational potential energy per unit volume (\(\rho g h\)) has the same value at all points along a streamline.
