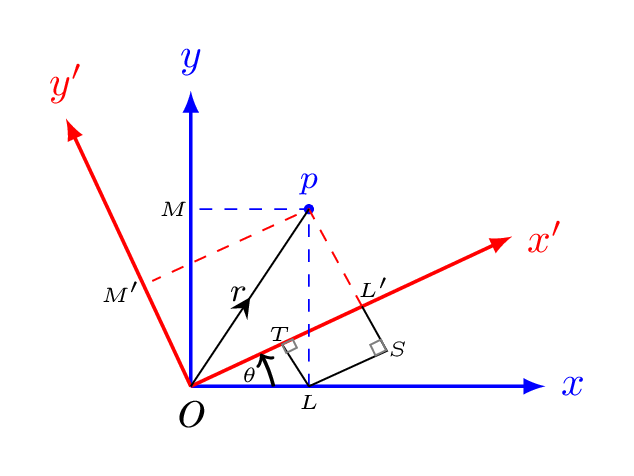
Subsection 2.1.3 Transformation of Axis
\begin{equation*}
x'=OL'= OT+TL' = OT +SL = OL\cos\theta +PL\sin\theta
\end{equation*}
\begin{equation*}
\therefore x' = x\cos\theta +y\sin\theta
\end{equation*}
\begin{equation*}
y'=PL'= PS-L'S =PS-TL = PL\cos\theta -OL\sin\theta
\end{equation*}
\begin{equation*}
\therefore y' = y\cos\theta -x\sin\theta
\end{equation*}
\begin{equation*}
\therefore \hat{i'}=\hat{i}\cos\theta +\hat{j}\sin\theta \qquad \text{also} \quad \hat{j'}=-\hat{i}\sin\theta +\hat{j}\cos\theta
\end{equation*}
Now,
\begin{equation*}
\vec{r}=\hat{i'}x'+\hat{j'}y'= [\hat{i}\cos\theta +\hat{j}\sin\theta]x'+[-\hat{i}\sin\theta +\hat{j}\cos\theta]y'
\end{equation*}
\begin{equation*}
\therefore \vec{r}=\hat{i}[x'\cos\theta -y'\sin\theta] +\hat{j}[x'\sin\theta +y'\cos\theta] =\hat{i}x+\hat{i}y
\end{equation*}
