Subsection 7.3.2 Rotational Energy, Work, and Power
Whenever a rigid body is set into rotation about an axis, work is done by the torques. Consider a rigid body pivoted at point \(O\) is acted upon by a force \(\vec{F}\) at point \(P\) so that it rotates by a small arc length \(\,ds,\) then work done by the force is given by
\begin{equation*}
\,dW = \vec{F}\cdot\vec{ds} =\vec{F}\cdot\left(\,d\vec{\theta}\times\vec{r}\right)
\end{equation*}
\begin{equation*}
=\,d\vec{\theta}\cdot \left(\vec{r}\times \vec{F}\right)
\end{equation*}
\begin{equation*}
[\because \vec{a}\cdot(\vec{b}\times\vec{c})= \vec{b}\cdot (\vec{c}\times\vec{a})
\end{equation*}
\begin{equation*}
\therefore W=\int \vec{\Gamma}\cdot\,d\vec{\theta}=\int\Gamma\,d\theta
\end{equation*}
Since the direction of the angular displacement is measured along the axis, and the torque is acting along the same direction on the body. If a constant torque acts on a rigid body which is rotating about a fixed axis, then from the principle of conservation of mechanical energy, assuming no loss due to friction, the work done by the torque will produce a change in the kinetic energy of the body given by
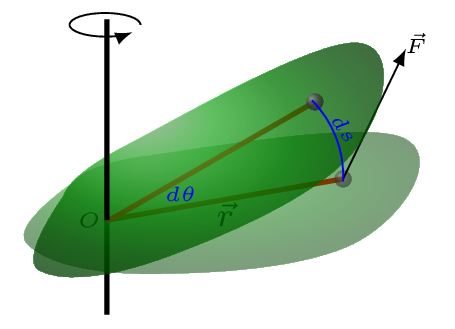
For maximum torque, \(\theta =90^{o}\text{,}\) and
\begin{equation*}
\Gamma =\vec{r}\times \vec{F} = rF\sin\theta = Fr.
\end{equation*}
\begin{equation*}
\,d W =Fr\,d\theta = \Gamma\,d\theta= I\alpha\,d\theta
\end{equation*}
\begin{equation*}
\,d K = \frac{1}{2}I\omega^{2}= \frac{1}{2}I\left(\omega^{2}_{f}-\omega^{2}_{i}\right)
\end{equation*}
\begin{equation*}
=\frac{1}{2}I \left(2\alpha\,d \theta\right)=I\alpha\,d\theta =\,d W
\end{equation*}
From rotational kinematics,
\begin{equation*}
\omega^{2}_{f}=\omega^{2}_{i}+2\alpha\theta.
\end{equation*}
where \(\omega_{f},\) and \(\omega_{i}\) are the final and initial angular velocity of the body, respectively and \(\theta\) is angular displacement through which the torque is applied.
