Subsection 7.3.3 Angular Momentum
A rigid body rotating with angular velocity, \(\omega\) about a fixed axis has an angular momentum \(L\) about this axis which is given by
\begin{equation*}
\vec{L}=I\vec{\omega}.
\end{equation*}
where \(I\) is the moment of inertia of the body about this axis. To change the angular momentum of a body, an external torque must be applied to it. Similar to
\begin{equation*}
F=\frac{\,dp}{\,dt} = ma,
\end{equation*}
in linear dynamics, we have in rotational dynamics
\begin{equation*}
\Gamma=\frac{\,dL}{\,dt} =I \alpha = I\frac{\,d\omega}{\,dt}.
\end{equation*}
That is, the torque acting on a rigid body is equal to the rate of change of the angular momentum. The direction of torque is along the change in angular momentum. The direction of angular momentum \(\vec{L}=I\vec{\omega}\) is along the angular velocity, which is along the axis of rotation. In the absence of external torques, the angular momentum of a rigid body must be constant, in other words, there is no change in the angular momentum when the sum of the external torques is zero. This is known as the principle of conservation of angular momentum, i.e., \(\Delta L =0.\) Similarly, the angular impulse
\begin{equation*}
\Delta J_{\theta} = \Gamma \Delta t =\Delta L.
\end{equation*}
Thus the change in angular momentum is equal to the angular impulse. Again,
\begin{equation*}
\vec{\Delta L}=\vec{r}\times\vec{F}\Delta t = \vec{r}\times\frac{\Delta p}{\Delta t}\Delta t=\vec{r}\times\vec{\Delta p}.
\end{equation*}
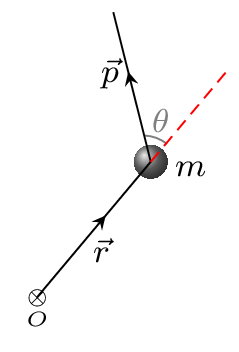
Hence angular momentum is also called moment of momentum. It is a vector quantity. It is acting along the direction perpendicular to the plane subtends by \(\vec{r}\) and \(\vec{v}.\) The angular momentum of a point particle is a measure of the circulation of the particle’s linear momentum about some specific point. In Figure 7.3.3, \(r\) is a position vector of mass, \(m\) measured from point \(O.\)
\begin{equation*}
|\vec{L}|= |\vec{r}\times\vec{p}| =| m\left(\vec{r}\times\vec{v}\right)| = mrv\sin\theta
\end{equation*}
here \(v\sin\theta \) is a component of velocity (or momentum) along position vector \(r\text{.}\) If the position vector and the velocity are contained in the x-y plane then the angular momentum is either along the +z axis or along the -z axis. If the right hand fingers pointed along the position vector curl along the velocity vector, then thumb will give the direction of angular momentum. In the Figure 7.3.3 if the right hand fingers are along the red dashed line curled towards the momentum vector then thumb is pointed out of the paper.
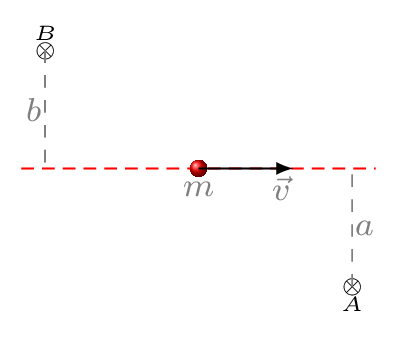
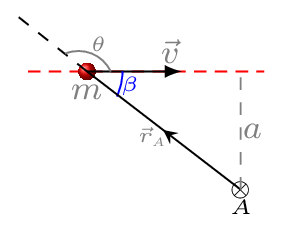
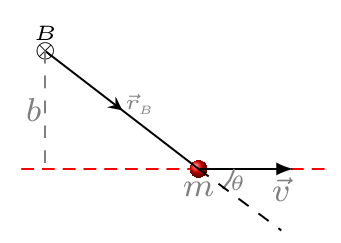
The angular momentum vector depends on the position vector of the point particle, therefore it depends on the point from which the particle’s position is measured. Consider a particle of mass \(m\) moving along the \(+x\) axis with velocity \(v\) as shown in Figure 7.3.4.(a), then the angular momentum of this particle is given with respect to points \(A\) and \(B\) are
\begin{equation*}
|\vec{L}_{A}| = |\vec{r}_{A}\times\vec{p}|
\end{equation*}
\begin{equation*}
= |m\vec{r}_{A}\times\vec{v}| = mr_{A}v\sin\theta =mr_{A}v\sin(180^{o}-\beta)
\end{equation*}
\begin{equation*}
=mr_{A}v\sin\beta = mr_{A}v\frac{a}{r_{A}}= mva
\end{equation*}
where \(\vec{L}_{A}\) is pointed into the paper [figure Figure 7.3.4.(b)]. Similarly,
\begin{equation*}
|\vec{L}_{B}| = |\vec{r}_{B}\times\vec{p}|
\end{equation*}
\begin{equation*}
= |m\vec{r}_{B}\times\vec{v}| = mr_{B}v\sin\theta = mr_{B}v\frac{b}{r_{B}}= mvb
\end{equation*}
and \(\vec{L}_{B}\) is pointed out of the paper [figure Figure 7.3.4.(c)].
