Skip to main content

General Physics I:

Sunil Karna

Section 5.5 Examples B

Example 5.5.1.

A body of mass \(m_{1}=1 \,kg\) traveling with a speed \(u_{1}=3 \,m/s\) collides with a stationary body of mass \(m_{2}=0.5 \,kg,\) and they stick together. What speed do the two bodies have after the collision?
Solution.
\begin{equation*} m_{1}u_{1}+0 = [m_{1}+ m_{2}] v \end{equation*}
\begin{equation*} \therefore v=\frac{m_{1}u_{1}}{m_{1}+m_{2}}=2 \,m/s \end{equation*}

Example 5.5.2.

Two initially stationary particles of mass 50 g are involved in an explosion that released 150 mJ of kinetic energy. What speed do they both have after the explosion?
Solution.
Given:
\begin{equation*} m_{1}=m_{2}=50\times10^{-3}\,kg, \quad u_{1}=u_{2}=0, \quad \Delta E = 150\times10^{-3} \,J \end{equation*}
\begin{equation*} \therefore 0=m_{1}v_{1} +m_{2}v_{2}\quad \Rightarrow\quad v_{1}=-v_{2} \end{equation*}
\begin{equation*} \text{also,}\quad 150\times10^{-3} =\frac{1}{2}m_{1}v_{1}^{2} +\frac{1}{2} m_{2}v_{2}^{2} \end{equation*}
\begin{equation*} \therefore \quad 3=v_{1}^{2} \quad \Rightarrow\quad v_{1}=\sqrt{3}=1.73 \,m/s \end{equation*}

Example 5.5.3.

A 10 kg mass traveling 2 m/s meets and collides elastically with a 2 kg mass traveling 4 m/s in the opposite direction. Find the final velocities of both objects.
Solution.
Given:
\begin{equation*} m_{1} = 10 \,kg,\quad m_{2} = 2\,kg, \quad u_{1}=2\,m/s, \quad u_{2}=-4\,m/s \end{equation*}
Now, from momentum conservation
\begin{equation*} m_{1}u_{1} + m_{2}u_{2}= m_{1}v_{1} + m_{2}v_{2} \end{equation*}
\begin{equation*} \therefore 6=5v_{1}+v_{2} \end{equation*}
and from kinetic energy conservation
\begin{equation*} \frac{1}{2}m_{1}u_{1}^{2} + \frac{1}{2}m_{2}u_{2}^{2}= \frac{1}{2}m_{1}v_{1}^{2} + \frac{1}{2}m_{2}v_{2}^{2} \end{equation*}
\begin{equation*} \therefore 36=5v_{1}^{2}+v_{2}^{2} \end{equation*}
Solving these two equations, we get -
\begin{equation*} v_{1}=0\,m/s, v_{2} =6 \,m/s \end{equation*}

Example 5.5.4.

In an accident the 190 kg car with velocity \(u_{A} = 30 \,km/h \) collides head on with the 280 kg car with velocity \(u_{B}=20 \,km/h\text{.}\) The coefficient of restitution of the impact is \(e = 0.15.\) The duration of the collision is \(0.22 \,s.\) What are the velocities of the cars immediately after the collision? Determine the magnitude of the average acceleration to which the occupants of each car are subjected.
Solution.
The velocities before collision are
\begin{equation*} u_{A} = 30 \,km/h = 30\times \frac{5}{18}\, m/s = 8.33 \,m/s, \end{equation*}
\begin{equation*} u_{B} = -20 \,km/h = -5.55 \,m/s. \end{equation*}
The coefficient of restitution, \(e = 0.15\text{.}\)
From momemtum conservation,
\begin{equation*} m_{A} u_{A} +m_{B} u_{B} =m_{A} v_{A} +m_{B} v_{B} \end{equation*}
\begin{equation*} \text{or,} \quad 190(8.33) +280(-5.55) = 190 v_{A} +280 v_{B} \end{equation*}
\begin{equation} \therefore \quad 19 v_{A} +28 v_{B} = 2.87\tag{5.5.1} \end{equation}
\begin{equation*} \text{also}\quad e =\frac{v_{B}-v_{A}}{u_{A}-u_{B}} \end{equation*}
\begin{equation*} \text{or,}\quad e (u_{A}-u_{B}) = v_{B}-v_{A} \end{equation*}
\begin{equation*} \text{or,}\quad 0.15(8.33+5.55) =v_{B}-v_{A} \end{equation*}
\begin{equation} \therefore \quad v_{B}-v_{A} =2.08\tag{5.5.2} \end{equation}
on Solving eqns. (5.5.1) and (5.5.2), we get the velocities after collision as \(v_{A}= -1.18 \,m/s,\) \(v_{B}= 0.9 \,m/ s.\) The average accelerations are
\begin{equation*} a_{A}=\frac{\Delta v}{\Delta t} = \frac{v_{A}-u_{A}}{\Delta t} =\frac{-1.18-8.33}{0.22} =-43.23 \,m/s^{2} \end{equation*}
\begin{equation*} a_{B}=\frac{\Delta v}{\Delta t} = \frac{v_{B}-u_{B}}{\Delta t} =\frac{0.9-(-5.55)}{0.22} =29.32 \,m/s^{2} \end{equation*}

Example 5.5.5.

A baseball of mass 300 g thrown at a speed of 50 m/s hits a bat of mass 3 kg moving in the opposite direction at 25 m/s. After being in contact with the bat for 1 ms, the ball rebounds with a speed of 60 m/s.
  1. What is the impulse delivered to the ball?
  2. What is the average force exerted by the bat on the ball during the collision?
  3. What is the speed of the bat immediately after the collision?
Solution.
  1. \(m_{1} = 0.3 \,kg, \quad v_{1i} = 50\, m/s,\quad v_{1f} = -60 \,m/s, \) \(p_{1i} = m_{1} v_{1i} = 15 \,kg.m/s,\quad p_{1f} = m_{1} v_{1f} = -18\, kg.m/s,\) \(\Delta p_{1} = p_{1f} - p_{1i} = -33 \,kg.m/s,\) \(\therefore J_{1} = \Delta p_{1} = -33 \,N.s\)
  2. \(\displaystyle t = 1\times 10^{-3} \,s,\quad J_{1} = F_{avg}t,\quad F_{avg} = -3.3\times 10^{4} \,N.\)
  3. \(v_{2i} = -25 \,m/s, \quad m_{2} = 3 \,kg,\quad p_{2i} = m_{2} v_{2i} = -75 \,kg.m/s, \) \(\Delta p_{2} = - \Delta p_{1} = 33 \,kg.m/s,\) \(\Delta p_{2} = p_{2f} - p_{2i},\quad p_{2f} = -42 \,kg.m/s,\quad p_{2f} = m_{2} v_{2f}, \) \(v_{2f} = -14 \,m/s.\)

Example 5.5.6.

A mass of 2 kg moving to the right with a speed of 40 m/s collides with a second mass of 3 kg moving to the left with a speed of 10 m/s. For each of the following three cases find
  1. the final velocity of each mass,
  2. the coefficient of restitution, and
  3. the energy loss during the collision.
Solution.
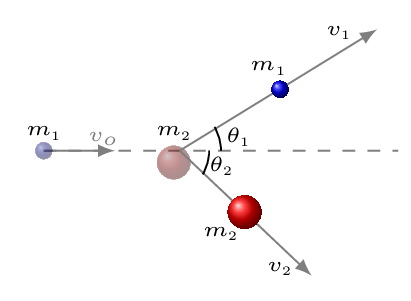
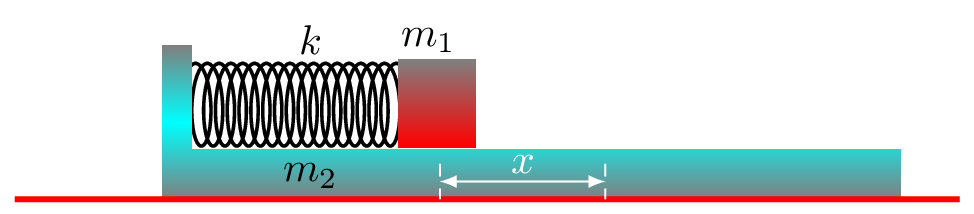
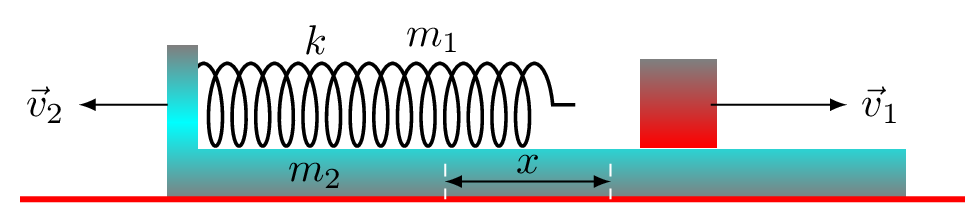
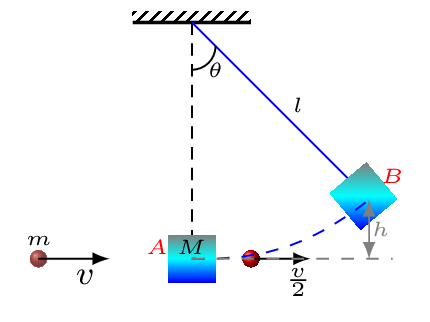
Case I: Perfectly inelastic collision.
Given: \(m_{1} = 2 \,kg,\quad v_{1i} = 40 \,m/s, \quad m_{2} = 3 \,kg,\) \(\quad v_{2i} = 10 \,m/s,\quad v_{1f} = v_{2f} = v\)
  1. \begin{equation*} p_{i} = p_{f},\quad p_{i} = m_{1} v_{1i} - m_{2} v_{2i}, \quad p_{f} = m v_{f}, \end{equation*}
    \begin{equation*} m = m_{1} + m_{2}, \quad v_{f} = 10 \,m/s \end{equation*}
  2. \begin{equation*} e = \frac{v_{sep}}{v_{app}}= 0 \quad \text{(inelastic collision)} \end{equation*}
  3. \begin{equation*} \Delta E = E_{i} - E_{f},\quad E_{i} = \frac{1}{2}m_{1} v^{2}_{1i} + \frac{1}{2}m_{2} v^{2}_{2i}, \end{equation*}
    \begin{equation*} E_{f} = \frac{1}{2} m v_{f}^{2},\quad \Delta E = 1500 \,J \end{equation*}
Case II: The first mass stops.
Given:
\begin{equation*} m_{1} = 2 \,kg,\quad v_{1i} = 40 \,m/s,\quad m_{2} = 3\, kg, \quad v_{2i} = 10 \,m/s,\quad v_{1f} = 0 \end{equation*}
  1. \begin{equation*} p_{i} = p_{f},\quad p_{i} = m_{1} v_{1i} - m_{2} v_{2i},\quad p_{2f} = m_{2} v_{2f},\quad v_{2f} = 16.67 \,m/s \end{equation*}
  2. \begin{equation*} e = \frac{v_{sep}}{v_{app}}, \quad v_{sep} = v_{2f}, \quad v_{app} = v_{1i} + v_{2i}, \quad e = 0.3333 \end{equation*}
  3. \begin{equation*} \Delta E = E_{i} - E_{f},\quad E_{i} = 1/2 m_{1} v^{2}_{1i} + 1/2 m_{2} v^{2}_{2i}, \end{equation*}
    \begin{equation*} E_{f} = 1/2 m_{2} v_{2_{f}}^{2}, \quad \Delta E = 1333\, J \end{equation*}
Case III: Perfectly elastic collision.
Given:
\begin{equation*} m_{1} = 2 \,kg,\quad v_{1i} = 40 \,m/s,\quad m_{2} = 3 \,kg,\quad v_{2i} = -10 \,m/s, \quad e = 1 \end{equation*}
  1. \begin{equation*} p_{i} = p_{f}, \quad p_{i} = m_{1}v_{1i} + m_{2} v_{2i}, \quad p_{f} = m_{1} v_{1f} + m_{2} v_{2f}, \end{equation*}
    \begin{equation*} \quad e = \frac{v_{sep}}{v_{app}}, \quad v_{sep} = v_{2f} - v_{1f}, \end{equation*}
    \begin{equation*} v_{app} = v_{1i}- v_{2i}, \quad v_{1f} = -20 \,m/s, v_{2f} = 30 \,m/s \end{equation*}
  2. \begin{equation*} e = 1\quad \text{(elastic collision)} \end{equation*}
  3. \begin{equation*} \Delta E = E_{i} - E_{f}, \quad E_{i} = 1/2 m_{1} v^{2}_{1i} + 1/2 m_{2} v^{2}_{2i}, \end{equation*}
    \begin{equation*} E_{f} = 1/2 m_{1} v^{2}_{1f} + 1/2 m_{2} v_{2f}^{2}, \quad \Delta E = 0 J \quad \text{(elastic collision)} \end{equation*}

Example 5.5.7.

A 5-g bullet moving north at 300 m/s ricochets off a 1 kg rock at a speed of 200 m/s in the northwest direction.
  1. With what speed and in what direction does the rock rebound?
  2. How much energy was turned into heat as a result of the collision?
Solution.
Given: \(m_{1} = 0.005 \,kg,\quad v_{1i} = 300 \,m/s, \quad v_{2i} = 0, \) \(m_{2} = 1 \,kg,\quad v_{1f} = 200 \,m/s, \quad \theta_{1} = 45^{o}.\)
  1. \begin{equation*} p_{xi} = p_{xf}, \quad p_{xi} = m_{1} v_{1i}, \end{equation*}
    \begin{equation*} p_{fx} = m_{1} v_{1f} \cos\theta_{1} + m_{2} v_{2f} \cos\theta_{2}, \quad p_{yi} = p_{yf}, \quad p_{yi} = 0, \end{equation*}
    \begin{equation*} p_{yf} = m_{1} v_{1f} \sin\theta_{1} - m_{2} v_{2f} \sin\theta_{2}, \quad v_{2f} = 0.177 m/s,\quad \theta_{2} = 53.2^{o} \end{equation*}
  2. \begin{equation*} \Delta E = E_{i} - E_{f},\quad E_{i} = 1/2 m_{1} v^{2}_{1i}, \end{equation*}
    \begin{equation*} E = 1/2 m_{1} v_{1f}^{2} + 1/2 m_{2} v_{2f}^{2}, \Delta E = 125 \,J \end{equation*}

Example 5.5.8.

A bullet of mass 0.1 kg moving horizontally embeds itself in a wooden block of mass 10 kg initially at rest and supported by a string of length 1 m. The block with the bullet inside recoils and swings upward through an angle of \(60^{o}\) before coming to rest. What was the initial speed of the bullet.
Solution.
Given:
\begin{equation*} m=0.1 \,kg, \quad M=10 \,kg,\quad l=1 \,m,\quad\theta=60^{o}. \end{equation*}
Equation:
\begin{equation*} v_{o}=\left(1+\frac{M}{m}\right)\sqrt{2gl(1-\cos\theta)} \end{equation*}
Answer.
\begin{equation*} y = 0.5 \,m, \quad v = 1 \,m/s, \quad v_{o} = 101 \,m/s \end{equation*}

Example 5.5.9.

A spring of a force constant \(k\) is compressed using a block of mass \(m_{1}\) to a distance \(x\text{.}\) The spring is fixed to a L-shaped block of mass \(m_{2}\) which is free to slid on frictionless ground surface as shown in figure below. There is friction between the two blocks, howewver and when the block 1 is released and spring reaches to its equilibrium position, then block 1 is moving leftward with velocity \(v_{1}\) and block 2 is moving rightward with velocity \(v_{2}.\)
  1. After the entire system comes to rest, blocks 1 and 2 have slid a distance \(d\) relative to each other. Find the distance \(d_{1}\) covered by the block 1 from its initial position.
  2. After the entire system comes to rest, blocks 1 and 2 have slid a distance \(d\) relative to each other. Find the coefficient of kinetic friction, \(\mu_{k}\) between blocks 1 and 2.
Solution.
  1. \begin{equation} d=d_{1}+d_{2}\tag{5.5.3} \end{equation}
    Since the center of mass of the system is at rest, we have
    \begin{equation*} m_{1}d_{1}=m_{2}d_{2} \qquad\Rightarrow\quad d_{2} =\frac{m_{1}d_{1}}{m_{2}} \end{equation*}
    \begin{equation} \therefore \quad d = d_{1}+\left[\frac{m_{1}d_{1}}{m_{2}}\right] = d_{1}\left[1+\frac{m_{1}}{m_{2}}\right]\qquad [\text{from eqn.(i)}] \tag{5.5.4} \end{equation}
    \begin{equation} \text{Hence,}\quad d_{1}= \left[\frac{m_{2}}{m_{1}+m_{2}}\right] d \tag{5.5.5} \end{equation}
  2. From principle of conservation of momentum,
    \begin{equation} m_{1}v_{1}=m_{2}v_{2} \qquad \Rightarrow\quad v_{2} = \frac{m_{1}v_{1}}{m_{2}} \tag{5.5.6} \end{equation}
    From principle of conservation of energy, we have -
    \begin{equation*} \frac{1}{2}kx^{2}-f_{1} d_{1}=\frac{1}{2}m_{2}v_{2}^{2} \end{equation*}
    \begin{equation*} \text{or,}\quad \frac{1}{2}kx^{2}-\mu_{k}m_{1}g d_{1}=\frac{1}{2}m_{2}\left(\frac{m_{1}v_{1}}{m_{2}}\right)^{2} \end{equation*}
    \begin{equation*} [\because f_{1}=\mu_{k}N_{1}=\mu_{k}m_{1}g] \end{equation*}
    \begin{equation*} \text{or,}\quad \frac{1}{2}kx^{2}-\mu_{k}m_{1}g d_{1}=\frac{1}{2}m_{1}^{2}v_{1}^{2}\left(\frac{m_{1}}{m_{2}}\right) \end{equation*}
    \begin{equation*} =\left(\frac{m_{1}}{m_{2}}\right)\left(f_{1} d_{1}\right) \left(\frac{m_{1}}{m_{2}}\right)\left(\mu_{k}m_{1}g d_{1}\right) \end{equation*}
    \begin{equation*} \text{or,}\quad \frac{1}{2}kx^{2} =\mu_{k}m_{1}g d_{1}\left[1+\frac{m_{1}}{m_{2}}\right] \end{equation*}
    \begin{equation*} =\mu_{k}m_{1}g d_{1}\left[\frac{d}{d_{1}}\right] =\mu_{k}m_{1}g d \end{equation*}
    \begin{equation} \therefore\quad \mu_{k}= \frac{kx^{2}}{2m_{1}gd} \tag{5.5.7} \end{equation}

Example 5.5.10.

A projectile of mass 10 kg is shot into the air with an initial speed of 100 m/s at an angle of \(60^{o}\) above the horizontal. At the very top of the trajectory, the projectile explodes into two fragments of equal mass, one of which falls straight down starting at rest.
  1. How high does the projectile go?
  2. How far has the projectile traveled horizontally when it reaches the top of its trajectory?
  3. What is speed of the projectile when it reaches the top of its trajectory?
  4. What is the velocity of the second fragment after the projectile explodes?
  5. How far from the original projectile launch point does the second fragment strike the horizontal ground.
Solution.
From the principle of conservation of momentum,
\begin{equation} m_{o}v_{ox}= m_{1}v_{1x}+m_{2}v_{2x}\qquad [\text{along x-axis}] \tag{5.5.8} \end{equation}
\begin{equation} m_{o}v_{oy}= m_{1}v_{1y}+m_{2}v_{2y}\qquad [\text{along y-axis}] \tag{5.5.9} \end{equation}
\begin{equation*} m_{o}v_{o}\cos\theta = \frac{m_{o}}{2}\times 0 +\frac{m_{o}}{2}\times v_{2x} \end{equation*}
\begin{equation} \therefore \quad v_{2x} = 2v_{o}\cos\theta =2\times100\times\cos60^{o}= 100 \,m/s\tag{5.5.10} \end{equation}
Now from equation of motion,
\begin{equation*} v_{y}^{top} = v_{oy}-gt_{rise}. \end{equation*}
Just before it explodes at top, we have -
\begin{equation*} 0=v_{o}\sin\theta - gt_{rise} \qquad [\because v_{y}^{top}=0.] \end{equation*}
\begin{equation} \therefore\quad t_{rise} = \frac{v_{o}\sin\theta}{g} = \frac{100\times\sin60^{o}}{9.8} = 8.8 sec =t_{fall} \tag{5.5.11} \end{equation}
  1. \begin{equation*} h=v_{0y}t_{rise}-\frac{1}{2}gt_{rise}^{2} =v_{0}\sin60^{o}t_{rise}-\frac{1}{2}gt_{rise}^{2} =382.6 \,m \end{equation*}
  2. \begin{equation*} x_{1} =v_{ox}t_{rise}=v_{o}\cos60^{o}(8.8)= 440\, m \end{equation*}
  3. \begin{equation*} v_{top}=0. \end{equation*}
  4. \begin{equation*} v_{2x}=2v_{ox} =100 \,m/s. \end{equation*}
  5. \begin{equation*} x=x_{1}+x_{2} =v_{ox}t_{rise} + v_{2x}t_{fall}=v_{o}\cos60^{o}(8.8)+100(8.8)=1320 \,m. \end{equation*}

Example 5.5.11.

A bullet of mass \(m\) is shot at speed \(v\) toward a pendulum block of mass \(M\text{.}\) The bullet penetrates through the block and emerges on the other side traveling at speed \(\frac{v}{2} \text{.}\)
  1. What is the speed of block immediately after the bullet emerges out from the block?
  2. What is the final height of block?
Solution.
  1. From the principle of conservation of momentum,
    \begin{equation*} p_{i}=p_{f} \end{equation*}
    \begin{equation*} \text{or,}\quad mv=MV+m\left(\frac{v}{2}\right) \end{equation*}
    \begin{equation*} \text{or,}\quad MV=mv-m\left(\frac{v}{2}\right) =m\left(\frac{v}{2}\right) \end{equation*}
    \begin{equation*} \therefore \quad V=\frac{mv}{2M} \end{equation*}
  2. From the principle of conservation of energy,
    \begin{equation*} E_{A}=E_{B}\qquad \text{or,}\quad \frac{1}{2}MV^{2} =Mgh \end{equation*}
    \begin{equation*} \text{or,}\quad h=\frac{V^{2}}{2g} =\frac{1}{2g}\left[\frac{m^{2}v^{2}}{4M^{2}}\right] = \frac{m^{2}v^{2}}{8M^{2}g} \end{equation*}

Example 5.5.12.

A ball is thrown from a table of height 2m horizontally with a velocity 3 m/s. Determine the distance D between the ball’s first and second bounces, if the coefficient of restitution is e = 0.6.
Solution.
Given: \(h=2m, \quad v_{x}=3m/s,\quad e=0.6. \) The vertical velocity after first bounce (impact) is given by
\begin{equation*} e=\frac{v_{sep}}{v_{app}} = \frac{v_{up}}{v_{down}} = \frac{v}{-u} \end{equation*}
\begin{equation} \therefore \quad v=-eu \tag{5.5.12} \end{equation}
From equation of motion,
\begin{equation*} v_{f}^{2}=v_{i}^{2}+2gh \end{equation*}
Final upward velocity becomes zero (\(v_{f}=v=0\)) after first bounce.
\begin{equation} 0=u^{2}-2gh \qquad \Rightarrow\quad u=\sqrt{2gh} \tag{5.5.13} \end{equation}
\begin{equation*} \therefore\quad v = -e\sqrt{2gh} =-0.6\times \sqrt{2\times9.8\times2} = 3.757 \,m/s \quad (upward) \end{equation*}
Hence the total height attained by the ball after first bounce can be determined by using conservation of energy principle.
\begin{equation*} \frac{1}{2}mv^{2}=mgh' \qquad \Rightarrow\quad h' = \frac{v^{2}}{2\,g} = \frac{e^{2}2gh}{2g}=e^{2}h=0.72 \,m \end{equation*}
Time to reach the highest point by the ball after first bounce is given by
\begin{equation*} v_{f}=v_{i}-gt \qquad \Rightarrow\quad 0 = v -gt \qquad \Rightarrow\quad t =\frac{v}{g}=\frac{3.757}{9.8} = 0.383 \,s \end{equation*}
Time to return by the ball to the ground for second bounce is given by \(T =2t= 0.767 \,s.\)
\begin{equation*} \therefore \quad D = v_{x}T = 3\times0.767 =2.30 \,m. \end{equation*}
PrevTopNext