Section 4.10 Center of Mass
The center of mass of a system of particles is a point in space at which the net mass of the system seems to be located. It is the mean position of the mass of a system or a body. Center of gravity is an imaginary point in a body where the entire weight of the body may be assumed to be concentrated or it is a point at which the gravity appears to act. In a uniform gravitational field the center of gravity is identical to the center of mass, but they do not coincide in a non-uniform gravitational field. Imagine that you are lying horizontally in space above the planet where you are experiencing a greater gravitational field strength towards your head than towards your feet, then your center of gravity is located somewhere near your shoulder rather than your belly button (i.e. navel or your center of mass). The center of gravity (or center of mass) may coincide with a geometric center of the body if it has a uniform mass distribution and possess symmetrical shape. An asymmetrical object composed of a variety of materials with different masses, however, has a center of gravity located at some distance from its geometric center. In some cases, such as hollow bodies or irregularly shaped objects, the center of gravity (or center of mass) may occur in space at a point external to the physical material. For example, the center of mass of binary stars lies between the stars and in the center of a tennis ball.
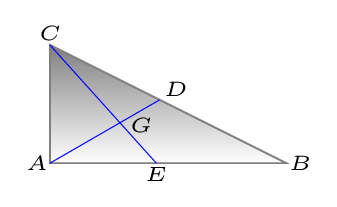
The center of (mass) gravity (point \(G\)) of any body can be determined by suspending the body by a cord attached at point \(A\) and then by a cord attached at \(C\text{.}\) When the body is suspended from \(A\text{,}\) the line \(AD\) is vertical; when it is suspended from \(C\text{,}\) the line \(CE\) is vertical. The center of gravity is at the intersection of \(AD\) and \(CE\) [Figure 4.10.1]. When an object is suspended from any single point, its center of gravity lies directly beneath that point. For a group of discrete masses the location of center of mass can be defined as:
\begin{equation*}
r_{cm} = \frac{\sum\limits_{i=1}^{n}{m_{i}r_{i}}}{\sum\limits_{i=1}^{n}{m_{i}}}
\end{equation*}
Vector position of center of mass.
or,
\begin{equation*}
r_{cm} = \frac{\int\limits_{0}^{M}{r\,dm}}{\int\limits_{0}^{M}{\,dm}} =\frac{1}{\int\limits_{0}^{M} \,dm} \int\limits_{0}^{M}{r\,dm} = \frac{1}{M} \int\limits_{0}^{M}{r\,dm}
\end{equation*}
or equivalently
\begin{equation*}
x_{cm} = \frac{\sum\limits_{i=1}^{n}{m_{i}x_{i}}}{\sum\limits_{i=1}^{n}{m_{i}}} = \frac{1}{M}\sum\limits_{i=1}^{n}{m_{i}x_{i}}\quad \text{(x-component of center of mass)}
\end{equation*}
\begin{equation*}
y_{cm} = \frac{\sum\limits_{i=1}^{n}{m_{i}y_{i}}}{\sum\limits_{i=1}^{n}{m_{i}}} = \frac{1}{M}\sum\limits_{i=1}^{n}{m_{i}y_{i}}\quad \text{(y-component of center of mass)}
\end{equation*}
\begin{equation*}
z_{cm} = \frac{\sum\limits_{i=1}^{n}{m_{i}z_{i}}}{\sum\limits_{i=1}^{n}{m_{i}}} = \frac{1}{M}\sum\limits_{i=1}^{n}{m_{i}z_{i}}\quad \text{(z-component of center of mass)}
\end{equation*}
Problem Solving Technique: To determine the center of mass of a uniformly distributed body, one performs the following steps:
- Break the body down into its constituent parts.
- Specify the length, area, or volume of each constituent part.
- Locate the coordinates of the center of mass of each constituent part.
- Utilize the equations shown above using length, area, or volume in place of the mass.\begin{equation*} e.g.,\quad x_{cm} = \frac{\sum\limits_{i=1}^{n}{A_{i}x_{i}}}{\sum\limits_{i=1}^{n}{A_{i}}} \end{equation*}for a unifrom sheet
- If an object has a uniform mass distribution (uniform density), then its geometric center is taken as center of mass.
