Subsection 7.5.4 Simple Pendulum with Large Angle Approximation
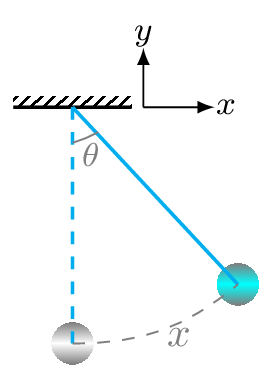
\begin{equation*}
x=l\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad \dot{x} =l\dot{\theta}
\end{equation*}
\begin{equation*}
V =-mgl\cos\theta
\end{equation*}
\begin{equation*}
K=\frac{1}{2}m\dot{x}^{2} = \frac{1}{2}ml^{2}\dot{\theta}^{2}
\end{equation*}
\begin{equation*}
T=K+V = \frac{1}{2}ml^{2}\dot{\theta}^{2}-mgl\cos\theta =const.
\end{equation*}
\begin{equation*}
\text{Now,}\quad \frac{\,dT}{\,dt} =0 =\frac{1}{2}ml^{2}2\dot{\theta}\ddot{\theta}+mgl\sin\theta\dot{\theta}
\end{equation*}
\begin{equation*}
\text{and}\quad \dot{\theta}\ddot{\theta} =-\frac{g}{l}\sin\theta\dot{\theta} \qquad [\because \theta \quad \text{is large}]
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\,d\theta}{\,dt}\left[\frac{\,d}{\,dt}\left(\frac{\,d\theta}{\,dt}\right)\right] =-\frac{g}{l}\sin\theta\left(\frac{\,d\theta}{\,dt}\right)
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\,d\theta}{\,dt}\left[\,d\left(\frac{\,d\theta}{\,dt}\right)\right] =-\frac{g}{l}\sin\theta\,d\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad \int\dot{\theta}\left(\,d\dot{\theta}\right) =-\frac{g}{l}\int\sin\theta\,d\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\dot{\theta}^{2}}{2}=\frac{g}{l}cos\theta+k. \qquad [\text{where k is a constant.}]
\end{equation*}
\begin{equation}
\text{or,}\quad \frac{\dot{\theta}^{2}}{2}-\omega^{2}cos\theta=k. \qquad \left[\because \omega=\sqrt{\frac{g}{l}}\right]\tag{7.5.9}
\end{equation}
This is a non-linear differential equation. At first extremum, \(\theta \to \theta_{i},\) and angular velocity at that moment is \(\dot{\theta}_{i}=0\) where \(i\) stands for maximum value of \(\theta.\)
\begin{equation*}
\text{or,}\quad 0 = \omega^{2}cos\theta_{i}+k
\end{equation*}
\begin{equation*}
\therefore\quad k = -\omega^{2}cos\theta_{i}
\end{equation*}
Therefore eqn. (7.5.9) becomes -
\begin{equation*}
\frac{\dot{\theta}^{2}}{2}=\omega^{2}cos\theta-\omega^{2}cos\theta_{i}
\end{equation*}
\begin{equation*}
\text{or,}\quad \dot{\theta} = \omega\sqrt{2\left(\cos\theta-\cos\theta_{i}\right)}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\,d\theta}{\,dt} = \omega \sqrt{2\left(\cos\theta-\cos\theta_{i}\right)}
\end{equation*}
At mean position at \(t=0,\theta=0,\) and \(\dot{\theta} \gt 0.\)
\begin{equation*}
\therefore\quad \int\limits_{0}^{t} \omega\,dt =\int\limits_{0}^{\theta_{i}} \frac{\,d\theta}{\sqrt{2\left(\cos\theta-\cos\theta_{i}\right)}}
\end{equation*}
Here,
\begin{equation*}
\left(\cos\theta-\cos\theta_{i}\right) =1-2\sin^{2}\frac{\theta}{2} - 1+2\sin^{2}\frac{\theta_{i}}{2}
\end{equation*}
\begin{equation*}
= 2\left(\sin^{2}\frac{\theta_{i}}{2} -\sin^{2}\frac{\theta}{2}\right)
\end{equation*}
\begin{equation*}
\therefore\quad \omega t =\frac{1}{2}\int\limits_{0}^{\theta_{i}} \frac{\,d\theta}{\sqrt{\left(\sin^{2}\frac{\theta_{i}}{2} -\sin^{2}\frac{\theta}{2}\right)}}
\end{equation*}
\begin{equation}
= \frac{1}{2}\int\limits_{0}^{\theta_{i}} \frac{\,d\theta}{\sin\frac{\theta_{i}}{2} \sqrt{\left( 1-\frac{\sin^{2}\frac{\theta}{2}}{\sin^{2}\frac{\theta_{i}}{2}}\right)}} \tag{7.5.10}
\end{equation}
Set
\begin{equation*}
\sin\phi= \frac{\sin\frac{\theta}{2}}{\sin\frac{\theta_{i}}{2}}
\end{equation*}
\begin{equation*}
\text{and say}\quad \sin\frac{\theta_{i}}{2} =b
\end{equation*}
and \(\sin\phi\) oscillates between \(-1 \quad\text{to}\quad +1.\) Now,
\begin{equation}
\sin\frac{\theta}{2} = b\sin\phi \tag{7.5.11}
\end{equation}
\begin{equation}
\therefore \quad \omega t= \frac{1}{2}\int \frac{\,d\theta}{b \sqrt{ 1-\sin^{2}\phi}} = \frac{1}{2}\int \frac{\,d\theta}{b \cos\phi} \tag{7.5.12}
\end{equation}
Differentiating eqn. (7.5.11), we get -
\begin{equation*}
\sin\frac{\theta}{2} =b\sin\phi
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{1}{2} \cos\frac{\theta}{2}\,d\theta = b\cos\phi\,d\phi
\end{equation*}
\begin{equation*}
\text{or,}\quad \,d\theta = \frac{2b\cos\phi\,d\phi}{\cos\frac{\theta}{2}}
\end{equation*}
From eqn. (7.5.12), we have -
\begin{equation*}
\omega t = \frac{1}{2}\int \frac{2b\cos\phi\,d\phi}{\cos\frac{\theta}{2}b\cos\phi}
\end{equation*}
\begin{equation*}
= \int \frac{\,d\phi}{\cos\frac{\theta}{2}} = \int \frac{\,d\phi}{1-\sin^{2}\frac{\theta}{2}}
\end{equation*}
\begin{equation}
\therefore\quad \omega t = \int \frac{\,d\phi}{1-b^{2}\sin^{2}\phi} \tag{7.5.13}
\end{equation}
This a first kind of elliptical integral.
From power series,
\begin{equation*}
\left(1-b^{2}\sin^{2}\phi\right)^{-\frac{1}{2}} = 1+\frac{1}{2}b^{2}\sin^{2}\phi+\frac{3}{2^{3}}b^{4}\sin^{4}\phi+\cdots
\end{equation*}
\begin{equation}
\therefore\quad \omega t = \int \left[1+\frac{1}{2}b^{2}\sin^{2}\phi+\frac{3}{8}b^{4}\sin^{4}\phi+\cdots\right]\,d\phi \tag{7.5.14}
\end{equation}
At \(t=0, \,\theta=0,\) the swing is at the lowest point, and hence \(\sin\phi=0\) \(\Rightarrow \phi=0\) see eqn.(7.5.11). Hence, from eqn. (7.5.14),
\begin{equation*}
\omega T_{1} = \int\limits_{0}^{2\pi}\,d\phi =2\pi
\end{equation*}
\begin{equation*}
\omega T_{2} = \int\limits_{0}^{2\pi}\frac{b^{2}}{2}\sin^{2}\phi\,d\phi
\end{equation*}
\begin{equation*}
=\int\limits_{0}^{2\pi}\frac{b^{2}}{2}\frac{\left(1-\cos2\phi\right)}{2}\,d\phi
\end{equation*}
\begin{equation*}
= \frac{b^{2}}{2}\pi = \frac{1}{2}\pi\sin^{2}\frac{\theta_{i}}{2}
\end{equation*}
\begin{equation*}
\omega T = 2\pi+\frac{\pi}{2}\sin^{2}\frac{\theta_{i}}{2} +\cdots
\end{equation*}
\begin{equation}
\therefore\quad T = 2\pi\sqrt{\frac{l}{g}}\left[1+\frac{1}{4}\sin^{2}\frac{\theta_{i}}{2}+\cdots \right]\tag{7.5.15}
\end{equation}
