Subsection 9.5.2 Equivalence between surface tension and surface energy
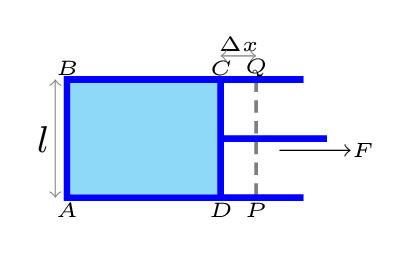
The natural tendency of a liquid is to contract its surface area to minimum its size. Therefore, work is required to increase the surface area of a liquid film. Increasing the surface area increasing the energy of the film. Hence, surface tension is the energy (or work) required to increase the surface area of a liquid by unit. Consider a thin film of liquid, ABCD, contained in a rectangular wire frame of movable side CD, as shown in Figure 9.5.4.
Now consider that the film is stretched by moving the side CD of the frame by \(\Delta x\) to the new position PQ. If \(\gamma\) is the surface tension of the liquid and a force \(F\) is applied, then work done by the force to stretch the film,
\begin{equation*}
W = F\Delta x = 2 \gamma l \Delta x
\end{equation*}
The factor 2 is taken because of two open surface area of the film on both sides of wire mesh. If \(\Delta A = 2 l \Delta x \) be the increased surface area of the film, then
\begin{equation*}
W = \gamma \Delta A
\end{equation*}
\begin{equation*}
\therefore\quad \gamma = \frac{W}{\Delta A}
\end{equation*}
Therefore, surface tension can also be defined in terms of energy, it is the ratio of change in surface energy to the change in surface area of the film. The surface tension is greatly dependent on temperature, so the definition of surface tension in terms of work per unit area is very useful in thermodynamics. The SI unit, in that case, is \(J/m^{2}.\)
