Subsection 10.5.2 Degree of Freedom:
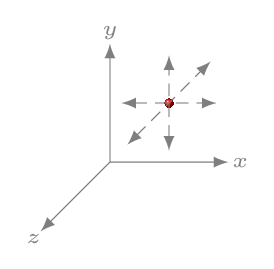
The degree of freedom is the number of independent motions possible to a particle or the number of independent coordinates required to specify particle’s dynamic position or the number of independent ways of exchanging particle’s energy. It depends on the atomic arrangement of an ideal gas molecule and types of motion it could have in the container. For example, it could have the combination of translation, rotational, and vibrational motion. For a monoatomic gas molecules (like helium, argon), consists of a single atom and can be represented by a point in space [Figure 10.5.2.(a)]. Such molecule therefore can have only translational motion in any of x-,y-,and z- direction. Thus it can have three independent motion and hence three degrees of freedom.
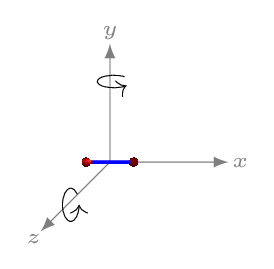
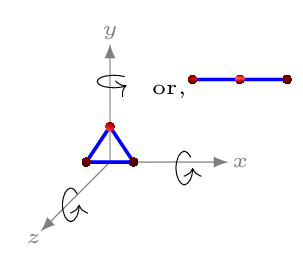
The molecule of a diatomic gas (like hydrogen, oxygen) is made up of two atoms joined rigidly like a dumbbell [Figure 10.5.2.(b)]. Such a molecule can translate as well as rotate about any one of the three mutually perpendicular axes. However, rotational inertia about an axis along the rigid rod will be negligible as compared to the other two rotational axes. Hence it can have only two rotational motions and three translational motions. The degrees of freedom for diatomic molecule is therefore five. A triatomic molecule either have linear arrangement of atoms (like \(CO_{2}, \quad O=C=O\)) or tringular arrangement (like \(H_{2}O\)), hence it may have either 7 (3 rotational, 1 vibrational, and 3 translational motions) degrees of freedom or 6 (3 rotational, and 3 translational motions) [Figure 10.5.2.(c)]. If we consider each molecule has three translational motions \(N\text{,}\) and the atoms are constrained to move along the rigid support, \(d\) then degrees of freedom, \(f=N-d\text{.}\) Hence for monoatomic gas, \(f=3-0=3;\) for diatomic gas, \(f=6-1=5;\) and for triatomic gas, \(f=9-3=6,\) in triangular arrangement of atoms, and \(f=9-2=7,\) in linear arrangement of atoms.
\begin{equation*}
\text{Now,}\quad pV = \frac{2}{3}N\frac{1}{2}m\overline{v^{2}}=\frac{2}{3} \frac{3}{2} N k_{B}T= N k_{B}T
\end{equation*}
If the container has \(n\) moles of a gas, then total number of molecules in the container can be given as
\begin{equation}
N = n N_{A} \tag{10.5.7}
\end{equation}
where \(N_{A}=6.022\times10^{23}\) molecules/mole is known as Avogadro’s number. Hence, for n mole of a gas,
\begin{equation*}
pV= Nk_{B}T= nN_{A} k_{B}T = nR T
\end{equation*}
where \(R = N_{A} k_{B} \) or \(n R = N k_{B}\) and \(R = 8.314 J/mole K\) is known as universal gas constant. Hence,
\begin{equation}
pV=Nk_{B}T = nRT \tag{10.5.8}
\end{equation}
eqn. (10.5.8) is called the equation of state of an ideal gas.
\begin{equation*}
pV=\frac{1}{3}M\overline{v^{2}} = nRT
\end{equation*}
\begin{equation*}
\therefore\quad v_{rms} = \sqrt{\frac{3nRT}{M}}
\end{equation*}
and
\begin{equation*}
pV=\frac{1}{3}Nm\overline{v^{2}} = Nk_{B}T
\end{equation*}
\begin{equation*}
\therefore \quad v_{rms} = \sqrt{\frac{3Nk_{B}T}{m}}
\end{equation*}
If n=1 mole, then M is a molar mass and we get-
\begin{equation}
v_{rms} = \sqrt{\frac{3RT}{M}} \tag{10.5.9}
\end{equation}
and if N=1, then
\begin{equation}
v_{rms} = \sqrt{\frac{3k_{B}T}{m}} \tag{10.5.10}
\end{equation}
The eqn. (10.5.9) shows that \(v_{rms}\) of a gas is proportional to the square root of absolute temperature and inversely proportional to the square root of its molar mass. The eqn. (10.5.10) shows that \(v_{rms}\) of a gas is proportional to the square root of absolute temperature and inversely proportional to the square root of its molecular mass.
Note: Molar mass [Subsubsection 10.5.3.1] is the mass of one mole of a substance, while molecular mass is the mass of one molecule of a substance. For examples, mass of 1 mole of H-atom is 1.008 gram, mass of 1 H-atom is \(1.008 \,g/N_{A} = 1.67\times 10^{-24}\,g.\) Mass of 1 mole of \(H_{2}\) molecule is 2.016 gram, mass of 1 molecule of \(H_{2}=2.016 \,g/N_{A} = 3.34\times 10^{-24}\,g.\)
