Skip to main content

General Physics I:

Sunil Karna

Section 9.3 Examples A

Example 9.3.1.

A cylindrical bottle can hold 400 g of water when filled to a depth of 7.95 cm. Find its inner radius.
Solution.
If m is mass of water, V is its volume, and \(\rho\) is its density., then
\begin{equation*} m = V\rho =Ah\rho = \pi r^{2}h\rho \end{equation*}
where \(A=\pi r^{2}\) is inner area of cross-scetion of the cylinder of radius \(r\) and \(h\) is the height of water in the cylindrical bottle.
\begin{equation*} \therefore\quad r=\sqrt{\frac{m}{\pi h \rho}}= \sqrt{\frac{400 \,g}{3.14 (7.50 \,cm)( 1 \,g/cm^{3})}} =4 \,cm \end{equation*}

Example 9.3.2.

A girl is standing on her one foot which has high heeled shoes of surface area \(1.5 \,cm^{2}\text{.}\) If she weigh 75 kg calculate the pressure in Pascal exerted on the floor by the heel.
Solution.
Given: \(m=75 \,kg, \) \(g=9.8 \,m/s^{2}.\) \(A=1.5 \,cm^{2} = 1.5\times \left(\frac{1}{100}m\right)^{2} =0.00015 \,m^{2},\)
\begin{equation*} p=\frac{F}{A} =\frac{mg}{A}=\frac{75\times 9.8}{0.00015} =4.9\times10^{6} \,Pa \end{equation*}

Example 9.3.3.

A piston of a hydraulic system has a surface area of \(0.025 m^{2}\) and pushes the hydraulic fluid with a pressure of 20,000 pascals. What pressure pushes on another piston in the same system?
Solution.
Given: \(A_{1}=0.025 \,m^{2}, \quad p_{1} 20,000 \,Pa.\) From Pascal’s principle,
\begin{equation*} p_{1} = p_{2} \end{equation*}
So the other piston gets pushed by the same pressure.

Example 9.3.4.

The specific gravity of mercury is 13.6.
  1. What is the density of mercury in MKS units?
  2. How high in meter will atmospheric pressure push a column of mercury up an evacuated tube?
  3. How many meter deep into water must a swimmer go in order to experience an increase in pressure equal to one atmosphere?
  4. How large a force (in Newtons) is pushing inward on a submarine window 25 cm in diameter if the specific gravity of sea water is 1.03, the submarine is 1 km deep, and the pressure inside the submarine is 1 atm?
Solution.
Given: \(G_{Hg} = 13.6, \quad \rho_{o} = 1000 \,kg/m^{3}, \quad h=1 \,km,\quad d=25 \,cm=0.25 \,m,\) and \(SG_{sw} =1.03.\)
  1. \begin{equation*} SG_{Hg} = \frac{\rho_{Hg}}{\rho_{o}} \end{equation*}
    \begin{equation*} \therefore\quad \rho_{Hg} = SG_{Hg}\times \rho_{o} = 13.6\times 1000 = 13600 \,kg/m^{3} \end{equation*}
  2. Atmospheric pressure in mercury reservoir is equal to gauge pressure in evacuated tube. Hence,
    \begin{equation*} p_{o}=p=h\rho_{Hg} g \end{equation*}
    \begin{equation*} \therefore\quad h = \frac{p_{o}}{\rho_{Hg} g} = \frac{1.01\times10^{5}N/m^{2}}{13600kg/m^{3}\times9.8 m/s^{2}} = 0.757 \,m \end{equation*}
  3. \begin{equation*} h= \frac{p}{\rho_{o} g} = \frac{p_{o}}{\rho_{o} g}=\frac{1.01\times10^{5}N/m^{2}}{1000kg/m^{3}\times9.8 m/s^{2}} = 10.30 \,m \end{equation*}
  4. \begin{equation*} F_{net}=pA=\left(p_{water}-p_{air}\right)A \end{equation*}
    \begin{equation*} But, \quad p_{water} = p_{o}+h\rho_{sw}g \end{equation*}
    and
    \begin{equation*} p_{o}=p_{air}=1 \,atm \end{equation*}
    \begin{equation*} \therefore\quad F_{net}=(h\rho_{sw} g)\left(\frac{\pi d^{2}}{4}\right) \end{equation*}
    \begin{equation*} = (1000m\times 1030 kg/m^{3}\times 9.8m/s^{2}) \left(\frac{\pi 0.25^{2}m^{2}}{4}\right) = 4.6\times 10^{5} \,N \end{equation*}

Example 9.3.5.

A 1.10 kg hollow steel ball is submerged in water. Its weight in water is 8.75 N. what is the volume of the cavity inside the ball, if density of steel is \(7,900 \,kg/m^{3}\text{?}\)
Solution.
Given: Mass of steel ball, m=1.10 kg, its weight in water, w’=8.75N, and its density, \(\rho_{s} =7900 \,kg/m^{3}.\) Suppose w and w’ are weights of the ball in air and in water, respectively. B is the bouyant force which is equal to the weight of displaced liquid. Since body loses weight due to buoyant force it is also equal to the weight loss of a body in the liquid. That is,
\begin{equation*} B = V_{b}\rho_{o}g = w-w' \end{equation*}
The ball is totally submerged in water, volume of liquid displaced is the same as volume of ball itself. Hence \(V_{dw} = V_{b},\) \(\rho_{o}\) is the density of water and \(w-w'\) is weight loss of ball in water.
\begin{equation*} \text{or,}\quad V_{b}\rho_{o}g = w-w'=mg-8.75 \,N \end{equation*}
\begin{equation*} \text{or,}\quad V_{b} = \frac{mg-8.75 N}{\rho_{o}g} \end{equation*}
\begin{equation*} =\frac{1.10(kg)\times 9.8(m/s^{2})-8.75(N)}{1000(kg/m^{3})9.8(m/s^{2})} = 2.07\times10^{-4}m^{3} = 207 \,cm^{3} \end{equation*}
\begin{equation*} But, \quad V_{b}=V_{c}+V_{s} \end{equation*}
where, \(V_{c}\) and \(V_{s}\) are the volumes of cavity and steel in the ball.
\begin{equation*} \therefore \quad V_{c} = V_{b}-V_{s} = V_{b}-\frac{m}{\rho_{s}} \end{equation*}
\begin{equation*} = 2.07\times10^{-4} -\frac{1.10}{7900} =6.8\times10^{-5} m^{3}= 67.75 \,cm^{3} \end{equation*}

Example 9.3.6.

A robber takes a chest full of gold put it on their horse and ride off into the distance. The size of the chest is about 18 inches long, 10 inches wide, and 8 inches high.
  1. How many pounds would such a chest weigh if it were filled with gold (\(\rho = 19.3 g/ml\))?
  2. What would be the buoyant force (in pounds) on the chest if it were placed under water?
  3. What would be the apparent weight (in pounds) of the chest while under water?
Solution.
Given: \(\rho_{o}=62.43 \,lb/ft^{3},\quad V = lbh=(1.5 \,ft) (0.67 \,ft) (0.83 \,ft) =0.834 \,ft^{3},\) \(\rho_{g} = 19.3 \,g/ml = 19.3 \times 62.43 \,lb/ft^{3} = 1205 \,lb/ft^{3}.\)
  1. \begin{equation*} W=mg=V_{c}\rho_{g} g \end{equation*}
    \begin{equation*} = 0.834 ft^{3}\times 1205 lb/ft^{3}\times 32ft/s^{2} = 32159 \,pdl \quad (or, poundal) \end{equation*}
  2. \begin{equation*} B= wt. loss =V_{c} \rho_{o} g = 0.834 ft^{3}\times 62.43 lb/ft^{3}\times 32ft/s^{2}=1665 \,pdl \end{equation*}
  3. \begin{equation*} B=w-w'\quad \Rightarrow\quad w'=w-B =32159-1665 =30494 \,pdl \end{equation*}

Example 9.3.7.

The density of fresh water is \(1.0 \,g/cm^{3}\) and the specific gravity of ice is 0.917. What is the minimum surface area of a slab of ice 50 cm thick that would support a man weighing 75 kg?
Solution.
Given: \(\rho_{o}=1 \,g/cm^{3} = 1000 \,kg/m^{3}, \) \(SG_{ics} =0.917, \quad l=50 \,cm =0.5\,m,\) and \(m=75 \,kg.\) Density of ice, \(\rho_{i}=SG_{ice}\times\rho_{o} =917 kg/m^{3}.\)
Buoyant force = wt. of a man + wt. of submerged portion of ice.
For a minimum surface area consider the entire ice is suspended inside the surface of water.
\begin{equation*} B= mg+ Mg \end{equation*}
\begin{equation*} V_{dw}\rho_{o}g=mg+V_{ice}\rho_{ice}g \end{equation*}
\begin{equation*} V_{ice}\rho_{o}=m+V_{ice}\rho_{ice} \end{equation*}
As ice is completely submerged volume of displaced water \(V_{dw}\) is the same as volume of ice \(V_{ice}.\)
\begin{equation*} \therefore\quad V_{ice}[\rho_{o}-\rho_{ice}]=m \end{equation*}
\begin{equation*} \text{or,}\quad V_{ice}=\frac{m}{[\rho_{o}-\rho_{ice}]} = \frac{75}{(1000-917)}= 0.904 \,m^{3} \end{equation*}
but
\begin{equation*} V_{ice}=A_{ice}\times l = 0.904 \end{equation*}
\begin{equation*} \therefore\quad A_{ice} = \frac{0.904}{l} = \frac{0.904}{0.5} \approx 1.8 m^{2} \end{equation*}

Example 9.3.8.

A solid body when suspended by a string in air shows 40 N tension in the string. When it is completely submerged in water the tension in string will be 30 N and when it is completely submerged in unknown liquid, the tension will be 20 N. Find the density of unknown liquid.
Solution.
Given: Tension in string in air, T=40 N, tension in string in water, \(T_{1}=30\,N,\) and tension in string in unknown liquid, \(T_{2}=20N. \)
From first figure
\begin{equation} T = mg \tag{9.3.1} \end{equation}
From second figure
\begin{equation} T_{1} +B_{1}= mg \tag{9.3.2} \end{equation}
From third figure
\begin{equation} T_{2} +B_{2}= mg \tag{9.3.3} \end{equation}
From eqns. (9.3.1) and (9.3.2),
\begin{equation*} T_{1} +B_{1} =T \end{equation*}
\begin{equation*} \text{or,}\quad B_{1} = T-T_{1} \end{equation*}
\begin{equation*} \text{or,}\quad V_{b}\rho_{o}g =40-30 =10 \end{equation*}
\begin{equation*} \therefore\quad V_{b} =\frac{10}{\rho_{o}g} = \frac{10}{1000\times 9.8} = 1.02\times10^{-3} m^{3} \end{equation*}
From eqns. (9.3.1) and (9.3.3), we have -
\begin{equation*} T_{2} +B_{2} =T \end{equation*}
\begin{equation*} \text{or,}\quad B_{2} = T-T_{2} =40-20=20 \end{equation*}
\begin{equation*} \text{or,}\quad V_{b}\rho_{l}g =20 \end{equation*}
\begin{equation*} \therefore\quad \rho_{l} =\frac{20}{V_{b}g} = \frac{20}{1.02\times10^{-3}\times 9.8} = 2000 \,kg/m^{3} =2 \,g/ml \end{equation*}
alternate:
\begin{equation*} B=w-w' \end{equation*}
where \(w\) is a weight of a body in air and \(w'\) is a weight of a body in fluid.

Example 9.3.9.

A solid body of density \(\rho \) is suspended at the interface of two liquids. A liquid \(C\) is sitting on top of liquid \(D\) without mixing to each other and the specific gravity of liquids \(C\) and \(D\) is 0.8 and 1.2, respectively. If fraction of the volume of the body immersed in liquid \(D\) is \(\frac{\rho-2a}{a}\text{.}\) Find the value of \(a.\)
Solution.
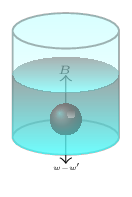
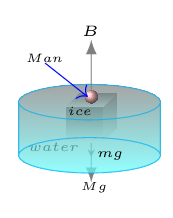
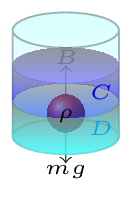
Given: \(\rho_{C} = 800 \,kg/m^{3}, \) \(\rho_{D} = 1200 \,kg/m^{3}, \quad \frac{V_{D}}{V}=\frac{\rho-2a}{a}.\) Specific gravity of a body, \(SG_{b}=\frac{\rho_{b}}{\rho}.\) Total volume of the body, \(V=V_{C}+V_{D}.\) Since the body is suspended at the interface of two liquids, buoyant force must be equal to its weight.
\begin{equation*} i.e., \quad B=mg \end{equation*}
\begin{equation*} \text{or,} \quad B_{C}+B_{D}=V\rho g \end{equation*}
\begin{equation*} \text{or,} \quad V_{C}\rho_{C}g+V_{D}\rho_{D}g=\left(V_{C}+V_{D}\right)\rho g \end{equation*}
\begin{equation*} \text{or,} \quad V_{C}\left(\rho_{C}-\rho\right)=V_{D}\left(\rho-\rho_{D}\right) \end{equation*}
\begin{equation} \text{or,} \quad V_{C} = \left(\frac{\rho-\rho_{D}}{\rho_{C}-\rho}\right) V_{D} \tag{9.3.4} \end{equation}
\begin{equation*} \text{But, }\quad \frac{V_{D}}{V} =\frac{\rho-2a}{a} \end{equation*}
\begin{equation} V_{D} = \left(\frac{\rho-2a}{a}\right)V \tag{9.3.5} \end{equation}
Hence, from
\begin{equation*} V=V_{C}+V_{D} = \left[\left(\frac{\rho-\rho_{D}}{\rho_{C}-\rho}\right) +1\right]V_{D} \end{equation*}
\begin{equation*} =\left[\left(\frac{\rho-\rho_{D}}{\rho_{C}-\rho}\right) +1\right] \left(\frac{\rho-2a}{a}\right)V \end{equation*}
\begin{equation*} \text{or,}\quad 1= \left[\left(\frac{\rho-\rho_{D}}{\rho_{C}-\rho}\right) +1\right] \left(\frac{\rho-2a}{a}\right) \end{equation*}
\begin{equation*} \therefore\quad a= \frac{\left(\rho_{C}-\rho_{D}\right)\rho}{3\rho_{C}-\rho-2\rho_{D}} \end{equation*}
\begin{equation*} = \frac{\left(800-1200\right)\rho}{3\times 800-\rho-2\times 1200} =400 \end{equation*}

Example 9.3.10.

A water rocket of length 20 cm and cross sectional area \(100 cm^{2}\) has half its volume initially filled with water. The air inside the rocket is pressurized to 10 atm and the area of the exhaust nozzle is \(1 cm^{2}\text{.}\)
  1. What is the initial exhaust velocity of the rocket?
  2. What is the initial volume flow rate for the rocket?
  3. What is the initial rate of decrease of mass of the rocket?
Solution.
Given: Length of the rocket, l=20cm = 0.2m, cross-sectional area of bottle, \(A_{1} =100 cm^{2} = 0.01m^{2},\) pressure inside the water bottle, \(p_{bot} = 10 atm=10 \times 1.01\times 10^{5} Pa,\) area of cross-section of nozzle, \(A_{2}= 1cm^{2} = 0.0001 m^{2}.\)
From Bernoulli’s principle,
\begin{equation*} p_{bot}+\rho gh_{1}+\frac{1}{2}\rho v_{1}^{2} = p_{o}+\rho gh_{2}+\frac{1}{2}\rho v_{2}^{2} \end{equation*}
\begin{equation} \text{or,}\quad \frac{p_{bot}-p_{o}}{\rho}+g\left(h_{1}-h_{2}\right) = \frac{1}{2}\left( v_{2}^{2}-v_{1}^{2}\right) \tag{9.3.6} \end{equation}
From equation of continuity,
\begin{equation*} A_{1}v_{1}=A_{2}v_{2} \quad \Rightarrow\quad v_{1}=\frac{A_{2}v_{2}}{A_{1}} \end{equation*}
\begin{equation*} \therefore\quad \frac{p_{bot}-p_{o}}{\rho}+g\left(h_{1}-h_{2}\right) \end{equation*}
\begin{equation*} = \frac{1}{2} v_{2}^{2}\left[1-\left(\frac{A_{2}}{A_{1}}\right)^{2}\right] \end{equation*}
  1. \begin{equation*} \therefore \quad v_{2} =\sqrt{\left[\frac{2\left(\frac{p_{bot}-p_{o}}{\rho}\right)+2g\frac{l}{2} }{\left(1-\left(\frac{A_{2}}{A_{1}}\right)^{2}\right)}\right]} = 42 m/s \end{equation*}
    Here \(\rho\) is density of water and \(h_{1}-h_{2}=\frac{l}{2}\text{.}\)
  2. initial volume flow rate,
    \begin{equation*} A_{2}v_{2} = 0.0001 \times 42 =0.0042 \,m^{3}/s \end{equation*}
  3. initial rate of decrease of mass,
    \begin{equation*} \frac{\,dm}{\,dt} = A_{2}v_{2}\rho = 0.0042\times 1000 = 4.2 \,kg/s \end{equation*}

Example 9.3.11.

A U-tube manometer is used to measure the pressure of oil of specific gravity 0.85 flowing in a pipe line. Its left end is connected to the pipe and right end is open to atmosphere. The center of the pipe is 100 mm below the level of mercury in the right limb. If the difference in mercury level in the two limbs is 160 mm. Find pressure at the center of the pipe.
Solution.
Given: \(\rho_{1}=0.85\times 1000 =850 \,kg/m^{3},\) \(d =100\times 10^{-3}m =0.10\,m,\) \(h_{2} =160\times 10^{-3}m = 0.16 \,m,\) \(h_{1} =160-100= 60 \,mm = 0.06 \,m,\) \(\rho_{2}=13.6\times 1000 =13600 \,kg/m^{3}.\)
\begin{equation*} p_{M}=p_{N} \end{equation*}
\begin{equation*} p_{A}+\rho_{1}g h_{1} = p_{o}+\rho_{2}g h_{2} \end{equation*}
\begin{equation*} p_{A}._{gauge} = p_{A}._{abs}-p_{o}=\rho_{2}gh_{2} -\rho_{1}gh_{1} \end{equation*}
\begin{equation*} \therefore\quad p_{A}._{gauge} = 13600\times 9.8 \times 0.16 -850\times 9.8 \times 0.1 = 20492 \,Pa \end{equation*}
PrevTopNext