Subsection 5.4.2 Ballistic Pendulum
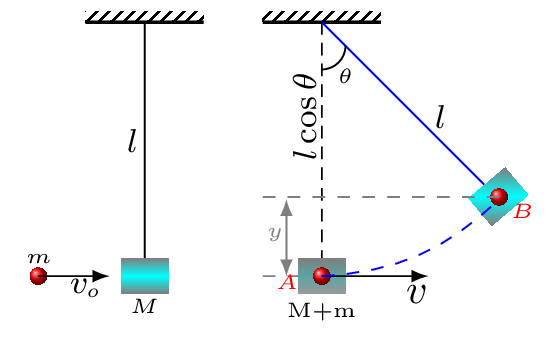
From the principle of conservation of momentum,
\begin{equation*}
\text{Momentum before collision = Momentum after collision.}
\end{equation*}
\begin{equation*}
mv_{o}+0 = (M+m)v
\end{equation*}
\begin{equation}
\therefore v=\frac{mv_{o}}{M+m} \tag{5.4.19}
\end{equation}
From the principle of conservation of energy,
\begin{equation*}
E_{A} = E_{B}.
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{1}{2}(M+m)v^{2}+0=0+(M+m) gy
\end{equation*}
\begin{equation}
\therefore v=\sqrt{2gy} \tag{5.4.20}
\end{equation}
\begin{equation*}
\frac{mv_{o}}{M+m} = \sqrt{2gy}
\end{equation*}
\begin{equation*}
\therefore \quad v_{o} = \left(\frac{M+m}{m}\right)\sqrt{2gy} = \left(1+\frac{M}{m}\right)\sqrt{2gy}
\end{equation*}
But
\begin{equation*}
y=l-l\cos\theta = l(1-\cos\theta).
\end{equation*}
\begin{equation}
\therefore \quad v_{o}=\left(1+\frac{M}{m}\right)\sqrt{2gl(1-\cos\theta)} \tag{5.4.21}
\end{equation}
Where \(v_{o}\) is called the muzzle velocity.
