Subsection 4.7.2 Vertical Circle
Consider a body of mass, \(m\) attached with a string of length, \(l\) and revolve in the vertical circle of radius, \(r\text{.}\) At any instant of time the body is at P such that string makes an angle \(\theta\) with the vertical. The weight (mg) of a body is acted downward which can be resolved into two components. One component \(mg\cos\theta\) is against tension \(T\) in the string and another component \(mg\sin\theta\) affect the speed of the body. Because of \(g\sin\theta\) body slows down as it goes up and speed up as it comes down. Hence the motion in a vertical circle is not uniform.
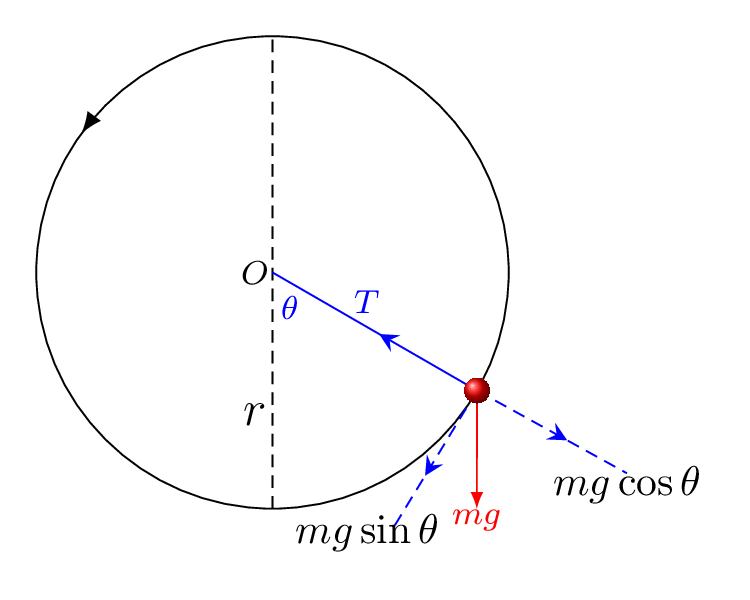
The necessary centripetal force in this case is provided by
\begin{equation*}
T-mg\cos\theta =\frac{mv^{2}}{r}
\end{equation*}
\begin{equation*}
\therefore T = m\left[\frac{v^{2}}{r}+g\cos\theta\right]
\end{equation*}
At \(\theta =0\text{,}\)
\begin{equation*}
T= m\left[\frac{v^{2}}{r}+g\right],
\end{equation*}
lowest point of ride.
At \(\theta =90^{o}\text{,}\)
\begin{equation*}
T= m\left[\frac{v^{2}}{r}\right],
\end{equation*}
quarter point of ride.
At \(\theta =180^{o}\text{,}\)
\begin{equation*}
T= m\left[\frac{v^{2}}{r}-g\right],
\end{equation*}
highest point of ride.
For a minimum velocity at the highest point \(T =0\text{,}\) hence
\begin{equation*}
\frac{v^{2}}{r}-g=0
\end{equation*}
\begin{equation}
or, \quad v=\sqrt{rg}\tag{4.7.3}
\end{equation}
