Skip to main content

General Physics I:

Sunil Karna

Section 7.4 Examples B

Example 7.4.1.

A body rotates according to the equation \(\theta = At + Bt^{3}\text{,}\) where \(A = 10 \,rad/s\) and \(B = 2 \, rad/s^{3}\text{.}\) Find:
  1. \(\displaystyle \theta(2s)\)
  2. \(\displaystyle \omega_{av}(0,2s)\)
  3. \(\displaystyle \omega(3s)\)
  4. \(\displaystyle \alpha_{av}(0,3s)\)
  5. \(\displaystyle \alpha(4s).\)
Solution.
Given: \(A = 10 \,rad/s,\, B = 2\, rad/s^{3} \)
  1. \begin{equation*} \theta(t) = A t + B t^{3}, \end{equation*}
    \begin{equation*} \therefore \theta(2s) = 10\times 2+ 2\times 2^{3} = 36\, rad. \end{equation*}
  2. \begin{equation*} \omega_{av} = \frac{\theta_{2}-\theta_{1}}{t_{2}-t_{1}}; \end{equation*}
    \begin{equation*} \therefore \omega_{av}(0,2\,s) = \frac{36-0}{2} = 18 \,rad/s \end{equation*}
  3. \begin{equation*} \omega(t) = \frac{\,d\theta}{\,dt} = A + 3 B t^{2}; \end{equation*}
    \begin{equation*} \therefore \omega(3\,s) = 10+3\times 2\times 3^{2} = 64 \,rad/s \end{equation*}
  4. \begin{equation*} \alpha_{av} = \frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}; \end{equation*}
    \begin{equation*} \therefore\alpha(0,3\,s) =\frac{64-10}{3} = 18 \,rad/s^{2} \end{equation*}
  5. \begin{equation*} \alpha (t) = \frac{\,d\omega}{\,dt} = 6 B t, \end{equation*}
    \begin{equation*} \therefore\alpha(4\,s) =6\times2\times4= 48 \, rad/s^{2}. \end{equation*}

Example 7.4.2.

A tire of mass 30 kg, radius of gyration 20 cm, and diameter 50 cm accelerates uniformly from rest. A small nail is embedded in the outer tread of the tire. After 100 revolutions the tire is rotating at 400 rpm. At that time, find each of the following:
  1. What is its angular acceleration?
  2. How much time did it take to get up to speed?
  3. What is the speed of the nail?
  4. What is the acceleration of the nail?
  5. What is the moment of inertia of the wheel?
  6. What torque is required to make the wheel rotate?
  7. How much energy was imparted to the wheel?
  8. How much power is required to rotate the wheel?
  9. What is the angular momentum of the wheel?
Solution.
Given:
\begin{equation*} m = 30 \,kg,\quad R = 0.2 m,\quad r = 0.25 \,m, \end{equation*}
\begin{equation*} \theta = 100 \, rev (2\pi rad/rev) = 628.3\, rad, \end{equation*}
\begin{equation*} \omega = 400 \,rpm (2 \pi/60 \,rad/s) = 41.89 \,rad/s,\quad \omega_{o}=0 \end{equation*}
  1. \begin{equation*} \omega^{2} = \omega^{2}_{o} + 2 \alpha\theta, \quad \alpha = 1.396 \,rad/s^{2} \end{equation*}
  2. \begin{equation*} \omega = \omega_{o} + \alpha t,\quad t = 30 \,s \end{equation*}
  3. \begin{equation*} v = r\omega = 10.47 \, m/s \end{equation*}
  4. \begin{equation*} a_{R} = r\omega^{2} = 438.7 m/s,\quad a_{T} = r \alpha = 0.349 \,m/s, \end{equation*}
    \begin{equation*} a = \sqrt{a_{R}^{2}+a_{T}^{2}} = 438.7 \,m/s \end{equation*}
  5. \begin{equation*} I = m R^{2} = 1.2 \,kg.m^{2} \end{equation*}
  6. \begin{equation*} \Gamma = I \alpha = 1.675 \,N.m \end{equation*}
  7. \begin{equation*} E = \frac{1}{2} I \omega^{2} = 1053\, J \end{equation*}
  8. \begin{equation*} P = \Gamma\omega = 70.16 \,W \end{equation*}
  9. \begin{equation*} L = I \omega = 50.27 \,kg.m^{2}/s \end{equation*}

Example 7.4.3.

An automobile engine with a moment of inertia of \(10 \,kg.m^{2}\) is revved up to 2400 rpm. The clutch is then popped and the car lurches forward. The effective moment of inertia of the clutch plate (including the gears, drive train, wheels, and mass of the car) is \(200 \,kg.m^{2}\text{.}\)
  1. What is the angular velocity of the clutch plate after the clutch is popped?
  2. If the gear ratio in the transmission is a 4 to 1 reduction, what is the angular velocity of the wheels after the clutch is popped?
  3. If the wheel has a radius of 30 cm, what is the speed of the car after the clutch is popped?
Solution.
  1. \begin{equation*} I_{1} = 10 \,kg.m^{2}, \quad\omega_{1} = 2400 \,rpm = 251.3 \,rad/s, \end{equation*}
    \begin{equation*} I_{2} = 200 \,kg.m^{2}, \quad I_{1} \omega_{1} = I_{2}\omega_{2},\quad \omega_{2} = 12.57 \,rad/s \end{equation*}
  2. \begin{equation*} \omega = \frac{1}{4} \omega_{2} = 3.142 \,rad/s \end{equation*}
  3. \begin{equation*} v = r \omega, \quad r = 0.3 \,m,\quad v = 0.9425 \,m/s \end{equation*}

Example 7.4.4.

The 20 kg disk of radius R = 0.25 m is at rest when the constant 10 N m counterclockwise torque is applied. Determine the disk’s angular velocity (in rpm) when it has rotated through four revolutions
  1. by applying the equation of angular motion \(\Gamma = I \alpha \) and
  2. by applying the principle of work and energy.
Solution.
Given: \(\theta = 4 rev = 4\times 2\pi = 8 \pi \,rad, \)
\begin{equation*} \Gamma = I\alpha = \frac{1}{2}MR^{2}\alpha\quad 10 \end{equation*}
\begin{equation*} =\frac{1}{2}20(0.25)^{2}\alpha \quad\Rightarrow\quad \alpha = 16 \,rad/s^{2} \end{equation*}
  1. Now,
    \begin{equation*} \alpha=\frac{\,d\omega}{\,dt} =\frac{\,d\omega}{\,d\theta}\frac{\,d\theta}{\,dt} =\omega\frac{\,d\omega}{\,d\theta} \end{equation*}
    \begin{equation*} \therefore \alpha\,d\theta = \omega\,d\omega \end{equation*}
    \begin{equation*} \text{or,}\quad \int\limits_{0}^{\theta} \alpha\,d\theta =\int\limits_{0}^{\omega} \omega\,d\omega \end{equation*}
    \begin{equation*} \text{or,}\quad \alpha \theta =\frac{\omega^{2}}{2} \end{equation*}
    \begin{equation*} \therefore \omega = \sqrt{2\alpha\theta} = \sqrt{2\times16\times 8\pi} = 28.36 \,(\frac{rad}{s}) \end{equation*}
    \begin{equation*} = 28.36 (\frac{rad}{s}) \times\frac{1}{2\pi}(\frac{rev}{rad-s})\times(\frac{60s}{1min}) = 271 \,\frac{rev}{min} \end{equation*}
  2. \begin{equation*} W=\frac{1}{2}I\omega^{2} \end{equation*}
    \begin{equation*} \text{or,}\quad \Gamma\theta = \frac{1}{2}I\omega^{2} \end{equation*}
    \begin{equation*} \text{or,}\quad 10\times 8\pi = \frac{1}{2}\left(\frac{1}{2}\times20\times 0.25^{2}\right)\omega^{2} \end{equation*}
    \begin{equation*} \therefore \omega = \sqrt{\frac{80\pi}{5\times0.25^{2}}} =28.36 \frac{rad}{s}=271 \,\frac{rev}{min} \end{equation*}

Example 7.4.5.

Two blocks of mass \(m_{1}\) and \(m_{2}\) are connected through a rope over a pulley of mass \(M\) and radius \(R.\) as shown in figure
. What is the acceleration of the blocks and the tension in the rope on either side of the pulley?
Solution.
From figure
.
\begin{equation} \sum F_{x} = T_{1}=m_{1}a \tag{7.4.1} \end{equation}
\begin{equation} \sum F_{y} =N=m_{1}g \tag{7.4.2} \end{equation}
Note: The tension on both sides a massive pulley must be different otherwise the pulley would not rotate. From figure
.
\begin{equation*} \sum \Gamma = T_{1}R-T_{2}R = -I\alpha \quad\text{clkwise rotation} \end{equation*}
\begin{equation*} \text{or,}\quad T_{1}-T_{2} = -I\frac{\alpha }{R} =-I\frac{a }{R^{2}} \qquad [\because a=R\alpha] \end{equation*}
\begin{equation} \therefore \quad T_{1}-T_{2} = -\frac{1}{2}MR^{2}\frac{a }{R^{2}} = -\frac{1}{2}Ma \tag{7.4.3} \end{equation}
From figure
\begin{equation*} \sum F_{y} =m_{2}g-T_{2} =m_{2}a \end{equation*}
\begin{equation} \therefore T_{2} = m_{2}g-m_{2}a\tag{7.4.4} \end{equation}
Now from eqns. (7.4.1) and (7.4.3),
\begin{equation*} m_{1}a- m_{2}g+m_{2}a = -\frac{1}{2}Ma \end{equation*}
\begin{equation*} \text{or,}\quad \left[m_{1} + m_{2} +\frac{1}{2}M\right]a= m_{2}g \end{equation*}
\begin{equation} \therefore \quad a =\frac{m_{2}g}{\left[m_{1} + m_{2} +\frac{1}{2}M\right]} \tag{7.4.5} \end{equation}
\begin{equation} \therefore T_{1} = m_{1}a = \frac{m_{1}m_{2}g}{\left[m_{1} + m_{2} +\frac{1}{2}M\right]}\tag{7.4.6} \end{equation}
\begin{equation} \therefore T_{2} = m_{2}g-m_{2}a = m_{2}g\left\{1-\frac{m_{2}}{\left[m_{1} + m_{2} +\frac{1}{2}M\right]}\right\} \tag{7.4.7} \end{equation}

Example 7.4.6.

A yo-yo has a mass \(M\text{,}\) a moment of inertia \(I\text{,}\) and an inner radius \(r.\) A string is wrapped around the inner cylinder of the yo-yo. A person ties the string to his finger and releases the yo-yo. As the yo-yo falls, it rolls on the string but does not slip. Find the acceleration of the yo-yo.
Solution.
\begin{equation} \sum F_{y} = mg-T =ma \quad \Rightarrow \quad T =mg-ma \tag{7.4.8} \end{equation}
\begin{equation*} \sum \Gamma = Tr =I\alpha \end{equation*}
\begin{equation} or, \quad T = \frac{I\alpha}{r} = \frac{Ia}{r^{2}} \quad [\because a=r\alpha] \tag{7.4.9} \end{equation}
From eqns. (7.4.8) and (7.4.9), we have -
\begin{equation*} mg=\frac{Ia}{r^{2}} +ma \end{equation*}
\begin{equation*} \therefore\qquad a = \frac{mg}{\left(\frac{I}{r^{2}} +m\right)} \end{equation*}

Example 7.4.7.

A bucket of water of mass 10 kg is supported by a rope wrapped around a uniform cylinder of mass 20 kg and radius 10 cm as shown in the [Figure a]. If the system is released from rest, how long it takes the bucket to fall to the bottom of a well 3 m deep?
Solution.
Given: \(M=20\,kg,\quad m=10\,kg, \quad h=3\,m, \quad R=10\,cm=0.1\,m, \) and \(v_{o}=0.\) Now, from free-body diagram [Figure b],
\begin{equation*} \sum F_{y}= mg-T=ma \end{equation*}
\begin{equation} \therefore \quad T=mg-ma \tag{7.4.10} \end{equation}
From free-body diagram [Figure c],
\begin{equation*} \sum\Gamma = TR=I\alpha = \frac{1}{2}MR^{2}\frac{a}{R} \qquad [\because a=R\alpha] \end{equation*}
\begin{equation} \therefore\quad T = \frac{M}{2}a \tag{7.4.11} \end{equation}
From eqns.(7.4.10) and (7.4.11), we have -
\begin{equation*} \frac{M}{2}a = mg-ma \end{equation*}
\begin{equation} \therefore\quad a = \frac{mg}{m+\frac{M}{2}} = \frac{10\times9.8}{10+\frac{20}{2}} =4.9\,m/s^{2}\tag{7.4.12} \end{equation}
Now well is 3m deep, so time taken by the block to reach at bottom of well is given by
\begin{equation*} h=v_{o}t+\frac{1}{2}at^{2} \end{equation*}
\begin{equation*} or,\quad 3=0+\frac{1}{2}\times 4.9 t^{2} \end{equation*}
\begin{equation*} \therefore\quad t = \sqrt{\frac{6}{4.9}} = 1.10 \,s \end{equation*}

Example 7.4.8.

A thin ring of mass 2 kg and diameter 10 cm rolls without slipping down an inclined plane 1 m long with one end 10 cm higher than the other. If the system is released from rest,
  1. What is the minimum coefficient of static friction that will cause the ring to roll without slipping?
  2. How long does it take for the ring to get to the bottom of the incline?
  3. How fast is the ring moving at that time?
  4. What fraction of the kinetic energy of the ring is due to its rotation at that time?
Solution.
Given: \(m=2\,kg, \quad w=mg, \quad R =\frac{d}{2} = \frac{10}{2} =5 \,cm =0.05\,m,\) \(l=1\,m, \quad h=10\,cm=0.1\,m, \quad v_{o}=0. \) From geometry of the figure,
\begin{equation*} \sin\theta = \frac{h}{l} =\frac{0.1}{1} =0.1 \end{equation*}
\begin{equation*} or,\quad \theta =\sin^{-1}(0.1) = 5.74^{o} \end{equation*}
\begin{equation} \sum F_{x} =w\sin\theta-f_{s} =ma \tag{7.4.13} \end{equation}
\begin{equation} \sum F_{y} =N-w\cos\theta =0 \tag{7.4.14} \end{equation}
\begin{equation} \text{but}\quad f_{s} =\mu_{s}N \tag{7.4.15} \end{equation}
\begin{equation} \text{and}\quad \Gamma = Rf_{s}=I \alpha\tag{7.4.16} \end{equation}
\begin{equation} \text{or,}\quad Rf_{s}=mR^{2} \frac{a}{R}\qquad \Rightarrow\quad f_{s} = ma \tag{7.4.17} \end{equation}
For ring \(I=mR^{2}\) and \(a=R\alpha.\) From eqns. (7.4.13) and (7.4.17), we get -
\begin{equation} mg\sin\theta =2 ma \qquad \Rightarrow\quad a = \frac{g\sin\theta}{2} =0.49m/s^{2} \tag{7.4.18} \end{equation}
Also from eqns. (7.4.14) and (7.4.15), we get -
\begin{equation} \mu_{s}mg\cos\theta = ma \qquad \Rightarrow\quad a = \mu_{s}g\cos\theta \tag{7.4.19} \end{equation}
  1. From eqns. (7.4.18) and (7.4.19), we get -
    \begin{equation*} \frac{g\sin\theta}{2} = \mu_{s}g\cos\theta \end{equation*}
    \begin{equation*} \therefore \quad \mu_{s} = \frac{\tan\theta}{2} = 0.05 \end{equation*}
  2. \begin{equation*} s=v_{o}t+\frac{1}{2}at^{2}\quad t=\sqrt{\frac{2s}{a}} = \sqrt{\frac{2\times 1}{0.49}} =2.02 s \end{equation*}
  3. \begin{equation*} v_{f}^{2}=v_{o}^{2}+2as \end{equation*}
    \begin{equation*} \therefore v_{f} = \sqrt{2as} =\sqrt{2\times0.49\times1} = 0.99 m/s \end{equation*}
  4. \begin{equation*} E_{top} =E_{bottom} \end{equation*}
    \begin{equation*} \text{or,}\quad mgh = \frac{1}{2}mv_{f}^{2}+ \frac{1}{2}I\omega_{f}^{2} \end{equation*}
    \begin{equation*} \therefore \quad \frac{KE_{rot}}{KE_{total}} = \frac{\frac{1}{2}mR^{2}\frac{v_{f}^{2}}{R^{2}}}{mgh} \end{equation*}
    \begin{equation*} =\frac{v_{f}^{2}}{2gh} = \frac{1}{2} \end{equation*}

Example 7.4.9.

A block of mass \(m_{b}\) and a disk of mass \(m_{d}\) and radius \(r\) are placed on a symmetric triangular slope connected with a massless string over a massless pulley [Figure (a)]. The string is connected to a center axle of the disk so that the disk is free to rotate. The moment of inertia of the disk about its axle is \(I =\frac{1}{2}m_{d}r^{2}.\) The coefficient of static friction between the slope and the block/disk is 0.05 and the coefficient of kinetic friction between the slope and the block/disk is 0.15. The angle \(\theta \) is \(30^{o}.\) Find the maximum ratio \(\frac{m_{b}}{m_{d}} \) such that the disk still rolls without slipping up the hill.
Solution.
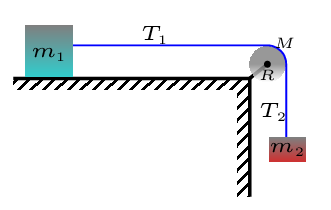
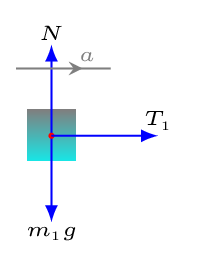
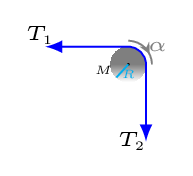
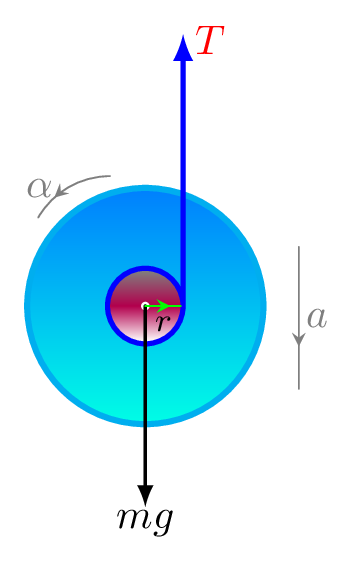
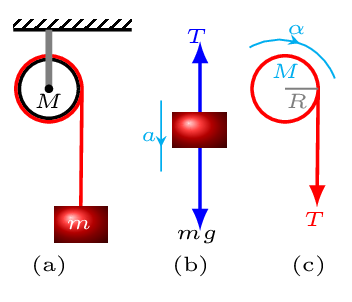
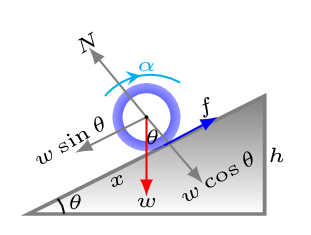
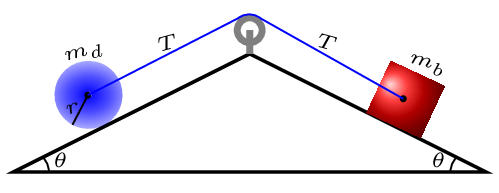
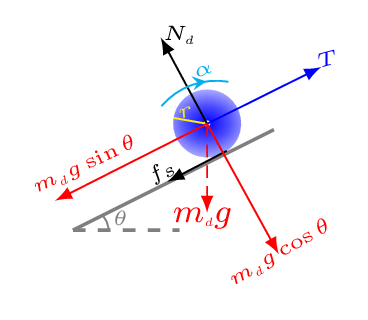
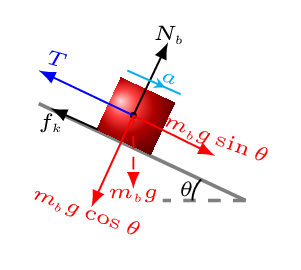
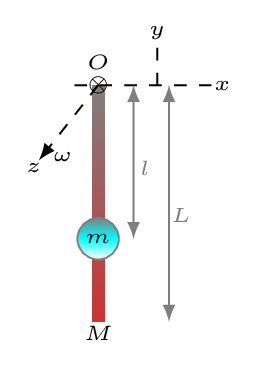
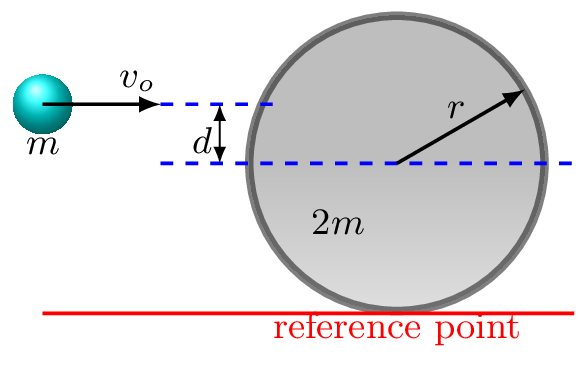
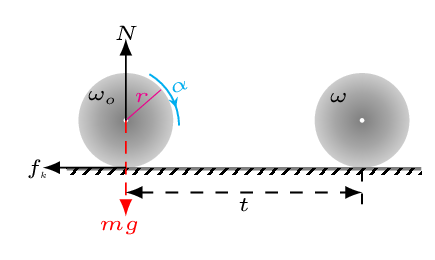
Since the disk is rolling without slipping, the maximum friction acting on the point of contact of disk and ramp must be static (i.e., \(0\leq f_{s}\leq \mu_{s}N\)). Now, whether the system is accelerating or not for the maximum ratio of \(\frac{m_{b}}{m_{d}} \) can be determined by the evaluation of final equation. From the free-body diagram construct equations as shown below. From [Figure (b)] consider the disk is accelerating upwards with an acceleration \(a\) for now, then
\begin{equation} \sum F_{x}= T-m_{d}g\sin\theta-f_{s}=m_{d}a \tag{7.4.20} \end{equation}
\begin{equation} \sum F_{y} = N_{d}-m_{d}g\cos\theta=0 \tag{7.4.21} \end{equation}
\begin{equation} \text{but,}\quad f_{s} = \mu_{s}N_{d}\tag{7.4.22} \end{equation}
\begin{equation} \text{and}\quad \sum\Gamma = -f_{s}r = -I\alpha \tag{7.4.23} \end{equation}
\begin{equation*} \therefore f_{s}r = I\alpha \end{equation*}
\begin{equation*} \text{or,}\quad \mu_{s}N_{d}r= \mu_{s}m_{d}g\cos\theta r= \frac{1}{2}m_{d}r^{2}\left(\frac{a}{r}\right)\quad [\because a=r\alpha] \end{equation*}
\begin{equation} \therefore\quad a=2\mu_{s}g\cos\theta = 2\times0.05\times9.8\times\cos(30^{o}) =0.85\,m/s^{2} \tag{7.4.24} \end{equation}
From [Figure (c)] the disk is accelerating downwards with an acceleration \(a\) because the block is connected to the disk through same rope via massless and frictionless pulley and hence has the same tension and acceleration, therefore
\begin{equation} \sum F_{x} = m_{b}g\sin\theta -f_{k}-T = m_{b}a \tag{7.4.25} \end{equation}
\begin{equation} \sum F_{y} = N_{b}-m_{b}g\sin\theta = 0 \tag{7.4.26} \end{equation}
\begin{equation} \text{but}\quad f_{k}=\mu_{k}N_{b} \tag{7.4.27} \end{equation}
Now from eqns. (7.4.20), (7.4.21) and (7.4.22), we get -
\begin{equation} T = m_{d}g\sin\theta +\mu_{s}m_{d}g\cos\theta +m_{d}a \tag{7.4.28} \end{equation}
and from eqns. (7.4.25), (7.4.26) and (7.4.27), we get -
\begin{equation} T = m_{b}g\sin\theta -\mu_{k}m_{b}g\cos\theta -m_{b}a \tag{7.4.29} \end{equation}
Hence from eqns. (7.4.28) and (7.4.29), and we have -
\begin{equation*} m_{b}\left[g\sin\theta -\mu_{k}g\cos\theta -a\right] = m_{d}\left[g\sin\theta +\mu_{s}g\cos\theta +a\right] \end{equation*}
\begin{equation*} \therefore \quad \frac{m_{b}}{m_{d}} = \frac{\left[g\sin\theta +\mu_{s}g\cos\theta +a\right]}{\left[g\sin\theta -\mu_{k}g\cos\theta -a\right] } \end{equation*}
\begin{equation*} = \frac{5.32+0.85}{3.63-0.85} = 2.22 \end{equation*}
If the system is not accelerating but moving with constant velocity, then \(a=0.\) Hence in that case
\begin{equation*} \frac{m_{b}}{m_{d}} = \frac{\left[g\sin\theta +\mu_{s}g\cos\theta \right]}{\left[g\sin\theta -\mu_{k}g\cos\theta \right] } \end{equation*}
\begin{equation*} =\frac{5.32}{3.63} = 1.46 \end{equation*}

Example 7.4.10.

The disk of mass 45 kg and radius R = 0.3 m is rolled to the left until the spring is compressed 0.5 m and then released from rest. If the spring constant is k = 600 N/m, and
  1. if the disk rolls without slipping, what is its angular acceleration at the instant it is released?
  2. What is the minimum coefficient of static friction for which the disk will not slip when it is released?
Solution.
Given: \(x_{o} =-0.5\,m,\quad m=45\,kg, \quad R=0.3\,m, \quad k=600\,N/m.\) From free-body diagram,
\begin{equation*} \sum F_{x} = F_{s}-f_{s} =ma\quad \text{and}\quad \sum F_{y} = N-mg =0 \end{equation*}
\begin{equation*} \sum \Gamma = -f_{s}R =-I\alpha \end{equation*}
\begin{equation*} or,\quad f_{s}R =\frac{1}{2}mR^{2}\frac{a}{R} \end{equation*}
\begin{equation*} \text{or,}\quad f_{s} =\frac{1}{2}ma \end{equation*}
  1. \begin{equation*} \text{or,}\quad F_{s}-\frac{1}{2}ma =ma \end{equation*}
    \begin{equation*} \text{or,}\quad a= \frac{2F_{s}}{3m} = \frac{-2 kx_{o}}{3m} = \frac{2\times 600\times 0.5}{3\times45}= 4.45 \,m/s^{2} \end{equation*}
    \begin{equation*} \therefore\quad \alpha = \frac{a}{R} = \frac{4.45}{0.3} = -14.81 \,rad/s^{2} \quad (clockwise) \end{equation*}
  2. \begin{equation*} F_{s}-f_{s} = ma = 2f_{s} \end{equation*}
    \begin{equation*} \text{or,}\quad -kx_{o} =3f_{s} = 3\mu_{s} N = 3\times\mu_{s}\times mg \end{equation*}
    \begin{equation*} \therefore\quad \mu_{s} = -\frac{kx_{o}}{3mg} =\frac{600\times 0.5}{3\times45\times9.8} = 0.23 \end{equation*}

Example 7.4.11.

A uniform disk of mass m and radius R is attached to the uniform rod of mass M and length L. The rod rotates with an angular speed \(\omega\) about an axis perpendicular to the xy-plane and that passes through one of its ends, point O as shown in figure. The center of mass of the disk is at a distance l with respect to point O. Calculate the angular momentum about this point.
Solution.
The angular momentum of a composite object is obtained as the sum of the angular momentum of each of its constituents.
\begin{equation*} L_{o} = L_{o}^{rod}+L_{o}^{disk} = I_{o}^{rod}\omega +I_{o}^{disk}\omega \end{equation*}
\begin{equation*} = \omega\left(I_{o}^{rod} + I_{o}^{disk}\right) \end{equation*}
The composites have same angular velocity, \(\omega\text{.}\) Now, moment of inertia of a rod about its end,
\begin{equation*} I_{o}^{rod} = \frac{ML^{2}}{3} \end{equation*}
Also, moment of inertia of a disk about point \(O\)using parallel axis theorem,
\begin{equation*} I_{o}^{disk} = \frac{1}{2}mR^{2}+ml^{2} \end{equation*}
\begin{equation*} \therefore \quad L_{o} = \left(\frac{ML^{2}}{3}+ \frac{1}{2}mR^{2}+ml^{2}\right)\omega \end{equation*}

Example 7.4.12.

A small ball of mass \(m\) traveling with initial velocity \(v_{o}\) hits a disk at rest of mass \(M=2m\) and radius \(r\) at a vertical distance \(d=\frac{r}{4}\) from the disk’s center. The ball bounces back horizontally with a velocity \(v_{b}\) and the disk begins rolling without slipping. Find the velocity of the disk after it has begun rolling without slipping.
Solution.
\begin{equation*} \Delta L = I\Delta\omega = r\Delta p \end{equation*}
\begin{equation*} \text{or,}\quad \left(I_{1}+I_{2}\right)(\omega_{f}-\omega_{i}) = \left(r+d\right)\left(p_{i}-p_{f}\right) \end{equation*}
\begin{equation*} \text{or,}\quad \left(\frac{1}{2}Mr^{2}+Mr^{2}\right)\omega_{f} = \left(r+\frac{r}{4}\right)\left[mv_{o}-(-mv_{b})\right] \end{equation*}
\([\because I=I_{cm}+mD^{2}]\)
\begin{equation*} \text{or,}\quad \frac{3}{2}Mr^{2}\left(\frac{v_{disk}}{r}\right) = \left(\frac{5r}{4}\right)\left[v_{o}+v_{b}\right]m \end{equation*}
\begin{equation*} \text{or,}\quad \frac{3}{2}(2m)rv_{disk} = \left(\frac{5r}{4}\right)\left[v_{o}+v_{b}\right]m \end{equation*}
\begin{equation*} \therefore\quad v_{disk} = \left(\frac{5}{12}\right)\left[v_{o}+v_{b}\right] \end{equation*}

Example 7.4.13.

A uniform thin rod of length \(L (m)\) and mass \(M (kg)\) can rotate in a horizontal plane about a vertical axis through its center. The rod is at rest when a bullet of mass \(m (kg)\) traveling in the horizontal plane of the rod is fired into one end of the rod. The direction of the bullet’s velocity makes an angle \(\alpha\) degrees with the rod. If the bullet lodges in the rod and the angular velocity of the rod is \(\omega\) rad/s immediately after the collision, what is the magnitude of the bullet’s velocity, \(v_{b}\) m/s just before impact? Determine the kinetic energy of the bullet before the collision and total rotational kinetic energy after the collision.
Solution.
\begin{equation*} L_{o} = L_{f} \end{equation*}
\begin{equation*} m(\vec{r}\times \vec{v}_{b}) +0 = I_{rod}\omega_{rod}+I_{b}\omega_{b} \end{equation*}
\begin{equation*} mv_{b}\frac{L}{2}\sin\alpha = \left[\frac{1}{12}ML^{2}+m\left(\frac{L}{2}\right)^{2}\right]\omega \end{equation*}
\begin{equation*} \therefore\quad v_{b}= \left[\frac{ML+3mL}{6m\sin\alpha}\right]\omega \end{equation*}
Kinetic energy of bullet before collision,
\begin{equation*} KE=\frac{1}{2}mv_{b}^{2} \end{equation*}
and total rotational kinetic energy after the collision,
\begin{equation*} KE_{rot} = \frac{1}{2}I_{rod}\omega^{2}+\frac{1}{2}I_{b}\omega^{2} \end{equation*}

Example 7.4.14.

A disk is spinning at a rate of 10 rad/s. A second disk of the same mass and shape, with no spin, is placed on top of the first disk. Friction acts between the two disks until both are eventually traveling at the same speed. What is the final angular velocity of the two disks?
Solution.
\begin{equation*} L_{o} = L_{f} \end{equation*}
\begin{equation*} I_{o}\omega_{o} = I_{f}\omega_{f} \end{equation*}
\begin{equation*} \therefore \omega_{f} = \frac{I_{o}\omega_{o} }{I_{f} } \end{equation*}
\begin{equation*} =\frac{I_{o}\omega_{o}}{I_{f}^{I disk}+I_{f}^{II disk}} \end{equation*}
\begin{equation*} =\frac{\frac{1}{2}MR^{2}10}{\frac{1}{2}MR^{2}+\frac{1}{2}MR^{2}} = 5 \,rad/s \end{equation*}

Example 7.4.15.

A particle attached to a string of length 2 m is given an initial velocity of 6 m/s. The string is attached to a peg and, as the particle rotates about the peg, the string winds around the peg. What length of string has wound around the peg when the velocity of the particle is 20 m/s?
Solution.
when string is winding around the peg its length decreases gradually causing the radius of rotation to decrease accordingly. Hence its moment of inertia decreases gradually and from conservation of angular momentum, angular velocity of the particle increases gradually.
\begin{equation*} L_{o} = L_{f} \end{equation*}
\begin{equation*} I_{o}\omega_{o} = I_{f}\omega_{f} \end{equation*}
\begin{equation*} I_{o}\frac{v_{o} }{R}= I_{f}\frac{v_{f} }{r} \end{equation*}
\begin{equation*} mR^{2}\frac{6}{2} = mr^{2}\frac{20 }{r} \end{equation*}
\begin{equation*} 3\times 2^{2} = 20r \qquad \therefore \quad r = \frac{3}{5} = 0.6\,m \end{equation*}
Hence \(2-0.6=0.4 m\) of string has already wound around the peg when the velocity is 20 m/s.

Example 7.4.16.

A rotating round object has an initial angular velocity \(\omega_{o}\) placed onto the horizontal surface. It rolls with slipping till achieve a final angular velocity \(\omega\text{.}\) If moment of inertia of the body is \(I = \gamma mr^{2}\text{.}\)
  1. Find \(\omega \text{.}\)
  2. If \(\omega = \frac{2}{5} \omega_{o}\) find the shape of the round object.
Solution.
when rotating object is placed on the surface its initial velocity \(v_{o} =0.\) Now due to frction translational velocity of the object is reduced after a time \(t\) when object starts rolling without slipping with an angular velocity \(\omega.\)
\begin{equation} v =v_{o}+at \tag{7.4.30} \end{equation}
\begin{equation*} f_{k} = ma = \mu_{k}mg \end{equation*}
\begin{equation} \Rightarrow a = \mu_{k}g \tag{7.4.31} \end{equation}
\begin{equation} \therefore \quad v = -\mu_{k}g \quad[\because \quad v_{o}=0] \tag{7.4.32} \end{equation}
also,
\begin{equation} \omega =\omega_{o}+\alpha t \tag{7.4.33} \end{equation}
\begin{equation*} \tau = I\alpha = f_{k}r \end{equation*}
\begin{equation} \therefore \quad \alpha = \frac{\mu_{k}mgr}{I} = \frac{\mu_{k}mgr}{\gamma mr^{2}} = \frac{\mu_{k}g}{\gamma r} \tag{7.4.34} \end{equation}
After time \(t\) on rolling without slipping,
\begin{equation*} v=r\omega \end{equation*}
\begin{equation*} -\mu_{k}g t =r\left(\omega_{o}+\alpha t \right) = r\left(\omega_{o}+\frac{\mu_{k}g t}{\gamma r} \right) \end{equation*}
\begin{equation*} \therefore\quad t = -\frac{r\omega_{o}\gamma}{\mu_{k}g (\gamma+1)} \end{equation*}
  1. \begin{equation*} \omega = \omega_{o} \left[\frac{\gamma }{\gamma +1}\right] \end{equation*}
  2. \begin{equation*} \frac{2}{5}\omega_{o}= \omega_{o}\left[\frac{\gamma }{\gamma +1}\right] \Rightarrow \gamma = \frac{2}{3} \end{equation*}
    Hence the round object is a hollow sphere.

Example 7.4.17.

Find the acceleration of a spherical ball rolling down the hill without slipping.
Hint.
\begin{equation*} \tau = I \alpha \end{equation*}
\begin{equation*} \tau = f\times r \end{equation*}
\begin{equation*} f=\mu N \end{equation*}
\begin{equation*} F=ma \end{equation*}
\begin{equation*} mg\sin\theta -f = ma \end{equation*}
\begin{equation*} \therefore\, a= \frac{5}{7} g\sin\theta \end{equation*}
PrevTopNext