Skip to main content

General Physics I:

Sunil Karna

Section 7.2 Examples A

Example 7.2.1.

Find the moment of inertia of the following mass distribution for the following axes,
  1. x,
  2. x’,
  3. y,
  4. z (out of the paper through the (x,y) origin).
Solution.
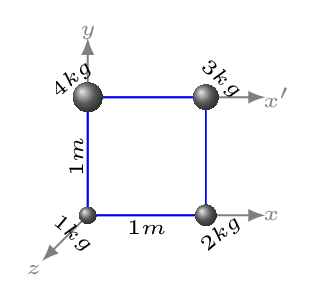
Given:
\begin{equation*} m_{1} = 1 \,kg, \quad m_{2} = 2 \,kg, \quad m_{3} = 3 \,kg,\quad m_{4} = 4 \,kg \end{equation*}
  1. \begin{equation*} r_{1} = 0, \quad r_{2} = 0 \,m, \quad r_{3} = 1 \,m,\quad r_{4} = 1 \,m \end{equation*}
    \begin{equation*} \therefore I_{x} = \sum\limits_{1}^{4} m_{i} r_{i}^{2} = 0+0+3\cdot 1^{2}+4\cdot 1^{2} = 7\, kg m^{2} \end{equation*}
  2. \begin{equation*} r_{1} = 1 \,m,\quad r_{2} = 1 \,m, \quad r_{3} = 0, \quad r_{4} = 0 \end{equation*}
    \begin{equation*} \therefore I_{x'} = \sum\limits_{1}^{4} m_{i} r_{i}^{2} = 1+2+0+0=3\, kg m^{2} \end{equation*}
  3. \begin{equation*} r_{1} = 0,\quad r_{2} = 1 \,m,\quad r_{3} = 1 \,m,\quad r_{4} = 0 \,m, \end{equation*}
    \begin{equation*} \therefore \quad I_{y} = \sum\limits_{1}^{4} m_{i} r_{i}^{2} = 0+2+3+0=5\, kg m^{2} \end{equation*}
  4. \begin{equation*} r_{1} = 0, \quad r_{2} = 1 \,m,\quad r_{3} = \sqrt{2}\, m,\quad r_{4} = 1\, m, \end{equation*}
    \begin{equation*} I_{z} = \sum m r^{2} = 12 \, kg m^{2} \end{equation*}

Example 7.2.2.

Two rods, each of mass m and length l, are welded together to form the T-shaped object. Use the parallel-axis theorem to determine the moment of inertia of the object about the axis through point O that is perpendicular to the bars.
Solution.
Divide the object into two pieces, each corresponding to a bar of mass m. Moment of inertia of first rod about its one end,
\begin{equation*} I_{1} =\frac{1}{3}ml^{2}. \end{equation*}
Moment of inertia of second rod about its center,
\begin{equation*} I_{2} =\frac{1}{12}ml^{2}. \end{equation*}
Moment of inertia of CM of second rod about point o using \(||^{l}\) axis theorem,
\begin{equation*} I_{2cm} =ml^{2}. \end{equation*}
\begin{equation*} \therefore I = I_{1}+(I_{2}+I_{2cm}) \end{equation*}
\begin{equation*} =\frac{1}{3}ml^{2}+ \frac{1}{12}ml^{2}+ml^{2} = \frac{17}{12}ml^{2} \end{equation*}

Example 7.2.3.

Calculate the moment of inertia of each of the uniform bodies
  1. uniform block about its long axis,
  2. square ring about its center, and
  3. hula hoop about its rim.
Solution.
  1. \begin{equation*} I = 1/12 M(a^{2} + a^{2}) = \frac{1}{6} M a^{2}; \end{equation*}
  2. \begin{equation*} I = 4 I_{1}, \, I_{1} = I_{1cm} + M_{1} R^{2}_{1},\, I_{1cm}= \frac{1}{12} M_{1} R^{2}_{1}, \end{equation*}
    \begin{equation*} M_{1} = M/4,\, R_{1} = L/2,\, I = \frac{13}{24} M L^{2}; \end{equation*}
  3. \begin{equation*} I = I_{cm} + M R^{2},\, I_{cm} = \frac{2}{5} M R^{2}, \, I = \frac{7}{5} M R^{2}. \end{equation*}

Example 7.2.4.

A rod of nonuniform mass distribution has a length, \(L\) and mass \(M\text{.}\) The linear mass density is given as \(\lambda = \lambda_{o}x\) where \(\lambda_{o}\) is constant.
  1. Find the center of mass of a rod.
  2. Find the moment of inertia of the rod about about an axis passing through one of its edges and perpendicular to its length.
Solution.
Linear mass density,
\begin{equation*} \lambda = \frac{\,dm}{\,dl}. \end{equation*}
\begin{equation*} or, \quad \,dm = \lambda \,dl = \lambda_{o} x \,dx. \end{equation*}
\begin{equation*} \therefore \quad M = \int \,dm = \int_{0}^{L} \lambda_{o} x \,dx \end{equation*}
\begin{equation*} = \lambda_{o} \left. \frac{x^{2}}{2}\right\vert_{0}^{L} = \frac{\lambda_{o}L^{2}}{2} \end{equation*}
\begin{equation*} Hence, \quad \lambda_{o} = \frac{2M}{L^{2}} \end{equation*}
  1. \begin{equation*} x_{cm} = \dfrac{\int_{0}^{M}x\,dm}{\int_{0}^{M}\,dm} = \frac{2}{\lambda_{o}L^{2}}\int_{0}^{L}x(\lambda_{o}x)\,dx = \frac{2}{3} L \end{equation*}
  2. \begin{equation*} \,dI = x^{2}\,dm = x^{2}\lambda \,dx = x^{2}\lambda_{o} x\,dx \ \end{equation*}
    \begin{equation*} \therefore \quad I = \int \,dI = \lambda_{o}\int_{0}^{L}x^{3} \,dx \end{equation*}
    \begin{equation*} = \lambda_{o}\left.\frac{x^{4}}{4} \right\vert_{o}^{L} = \frac{\lambda_{o}L^{4}}{4} = \frac{1}{2}ML^{2} \end{equation*}

Example 7.2.5.

A disk of nonuniform mass distribution has a radius, \(R\) mass and \(M\text{.}\) The surface mass density varies as \(\sigma = \sigma_{o} r^{2}\) where \(\sigma_{o}\) is a constant and \(r\) is measured from its center.
  1. Find its center of mass and
  2. moment of inertia about an axis passing through its geometric center and perpendicular to its plane.
Solution.
Surface mass density,
\begin{equation*} \sigma = \frac{\,dm}{\,dA}. \end{equation*}
\begin{equation*} or, \quad \, dm = \sigma \, dA = \sigma_{o} r^{2} (2\pi r \,dr) = 2\pi \sigma_{o}r^{3}\,dr \end{equation*}
\begin{equation*} \therefore\quad M = \int \,dm = 2\pi\sigma_{o}\int^{R}_{0} r^{3}\,dr = 2\pi\sigma_{o} \frac{R^{4}}{4} = \frac{1}{2}\pi \sigma_{o}R^{4} \end{equation*}
\begin{equation*} Hence, \quad \sigma_{o} = \frac{2M}{\pi R^{4}} \end{equation*}
  1. \begin{equation*} r_{cm} = \frac{1}{M}\int_{0}^{M}r\,dm = \frac{2}{\pi \sigma_{o}R^{4}} \int_{0}^{R}2\pi \sigma_{o}r^{4}\,dr = \frac{4}{5} R \end{equation*}
  2. \begin{equation*} \,dI = r^{2}\,dm =r^{2} 2\pi \sigma_{o}r^{3}\,dr \end{equation*}
    \begin{equation*} \therefore \quad I = \int \,dI = 2\pi\sigma_{o}\int_{o}^{R}r^{5}\,dr = \frac{1}{3}\pi\sigma_{o}R^{6} = \frac{2}{3}MR^{2}. \end{equation*}
PrevTopNext