Subsection 9.4.2 Poiseuille’s Law
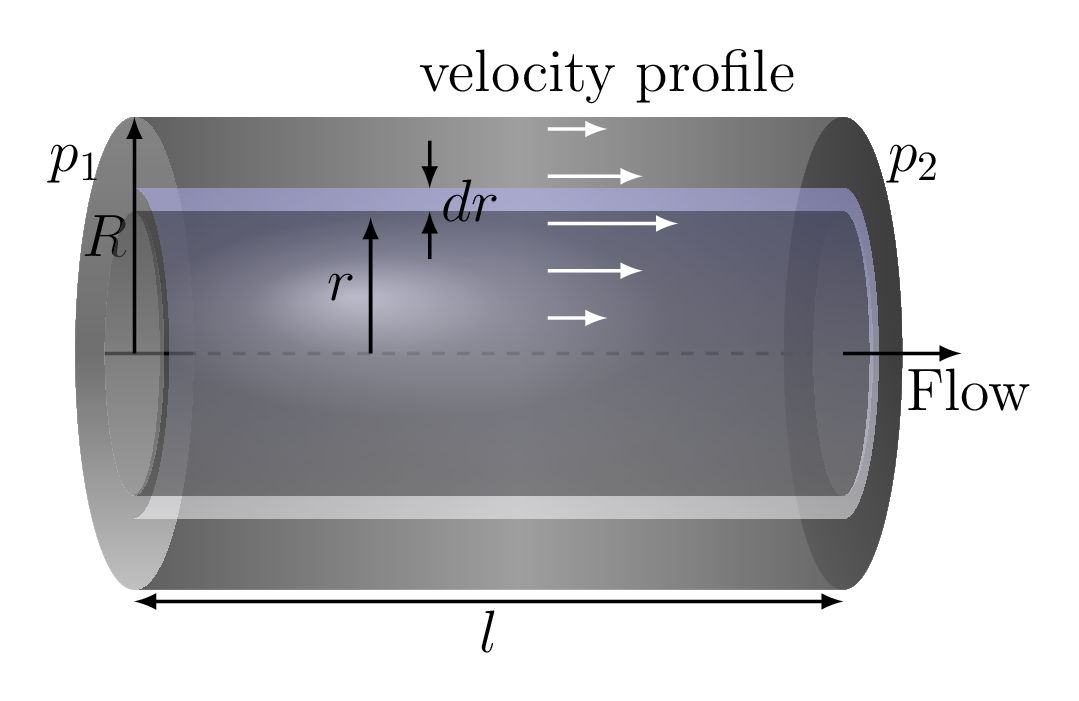
Liquid could flow in a tube freely but because of viscosity it needs pressure difference between the ends of the tube to flow. The rate of flow of fluid in a tube is dependent on its viscosity, pressure difference between the two ends of the tube (or, pressure gradient), and the radius of the tube. Posiseuille assume the laminar flow of incompressible fluid (mostly liquid) to obtain the Poiseuille’s equation.
Consider a uniform circular cylindrical tube of radius \(R\) and length \(l\) in which liquid has a laminar flow. Consider a layer of liquid at distance \(r\) from the center of the tube is moving with velocity \(v\text{,}\) then the viscous force acting on this layer is given by
\begin{equation}
F_{\mathrm{v}}=-\eta (2\pi rl)\frac{\,dv}{\,dr} \tag{9.4.1}
\end{equation}
\(-ve\) sign indicates that the viscous force is acting opposite to the direction of otion of the liquid, \((2\pi rl) \) is the surface area of the liquid, and \(\frac{\,dv}{\,dr} \) is the velocity gradient of the layer. The force due to pressure difference on the area of cross-section of the liquid is given by
\begin{equation}
F_{\mathrm{p}}=(p_{1}-p_{2})(\pi r^{2}) =\Delta p(\pi r^{2}) \tag{9.4.2}
\end{equation}
If the layer is moving with constant velocity, \(v\) then
\begin{equation*}
F_{\mathrm{p}}+F_{\mathrm{v}} =0
\end{equation*}
\begin{equation*}
\text{or,}\quad F_{\mathrm{p}}= -F_{\mathrm{v}}
\end{equation*}
\begin{equation*}
\text{or,}\quad \Delta p(\pi r^{2}) = \eta (2\pi rl)\frac{\,dv}{\,dr}
\end{equation*}
\begin{equation}
\text{or,}\quad \frac{\,dv}{\,dr} = \frac{\Delta p(\pi r^{2})}{\eta (2\pi rl)} = \left(\frac{\Delta p}{2\eta l}\right)r \tag{9.4.3}
\end{equation}
At axis of the tube, \(r=0,\)
\begin{equation*}
\frac{\,dv}{\,dr}=0
\end{equation*}
\(\Rightarrow \quad v \) is maximum, at \(r=R, \quad v=0\text{.}\) Integrating eqn. (9.4.3), we get -
\begin{equation*}
\int\limits_{v}^{0}\,dv = \left(\frac{\Delta p}{2\eta l}\right)\int\limits_{r}^{R}r\,dr
\end{equation*}
\begin{equation}
\therefore\quad v(r) = \left(\frac{\Delta p}{4\eta l}\right)(R^{2}-r^{2}) \tag{9.4.4}
\end{equation}
Eqn. (9.4.4) represents a parabolic (\(y\propto x^{2}\)) nature of velocity profile.
From equation of continuity, the rate of volume flow is given by
\begin{equation*}
\frac{\,dV}{\,dt} = \int (\vec{v}\cdot\,d\vec{A}) = \int v\,dA
\end{equation*}
The velocity and cross-sectional area of fluid are along the same direction.
\begin{equation*}
\frac{\,dV}{\,dt} = \int\limits_{0}^{R} \left(\frac{\Delta p}{4\eta l}\right)(R^{2}-r^{2})(2\pi r)\,dr
\end{equation*}
\begin{equation*}
= \left(\frac{\Delta p \pi}{2\eta l}\right) \int\limits_{0}^{R}(R^{2}r-r^{3})\,dr
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\,dV}{\,dt} = \left(\frac{\Delta p \pi}{2\eta l}\right)\left(\frac{R^{4}}{2}-\frac{R^{4}}{4}\right)
\end{equation*}
\begin{equation}
\therefore\quad \frac{\,dV}{\,dt} = \left(\frac{\pi \Delta p}{8\eta l}\right)R^{4} \tag{9.4.5}
\end{equation}
This is Poiseuille’s equation, also known as Poiseuille’s law.
