Subsection 10.6.5 Heat Engines
Heat engine is a device of converting heat continuously into work. The device absorbs heat from a high temperature reservoir, converts part of this energy into work and rejects the rest of the energy as heat to a low temperature drain. Hence, it consists of three essential parts: Source or reservoir for the supply of heat at high temperature. Sink or drain for the rejection of heat at lower temperature. Working Substance which absorbs heat from the source.
The working substance undergoes a cycle of operation in which it absorbs certain quantity of heat from the source, converts a part of it into work and rejected rest to the sink as shown in Figure 10.6.5. Finally it reaches to the initial stage where its internal energy is the same. By performing the same cycle again and again, heat is continuously converted into work.
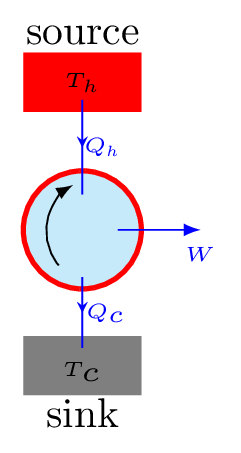
Efficiency: Let \(Q_{h}\) is the amount of heat absorbed by the working substance from the source at high temperature \(T_{h} \,K.\) It does the work W and reject \(Q_{c}\) amount of heat to the sink at lower temperature \(T_{c} \,K.\) The efficiency of the heat engine then defined as the ratio of the work done (output) by the engine to the amount of heat supplied (input) to the engine. That is,
\begin{equation*}
\eta = \frac{W}{Q_{h}}
\end{equation*}
If there is no dissipative losses (i.e., no frictional loss in engine, etc.) then heat rejected would be
\begin{equation*}
Q_{c}= Q_{h} - W
\end{equation*}
\begin{equation*}
\Rightarrow\quad W=Q_{h}-Q_{c}
\end{equation*}
Hence
\begin{equation*}
\eta = \frac{Q_{h}-Q_{c}}{Q_{h}}
\end{equation*}
\begin{equation*}
\therefore\quad \eta = \left(1-\frac{Q_{c}}{Q_{h}}\right)\times 100\%
\end{equation*}
Since, efficiency is normally defined in percentage.
