Subsection 10.6.8 Carnot’s Cycle:
The Carnot engine operates in the four steps of Carnot cycle which are perfectly reversible.
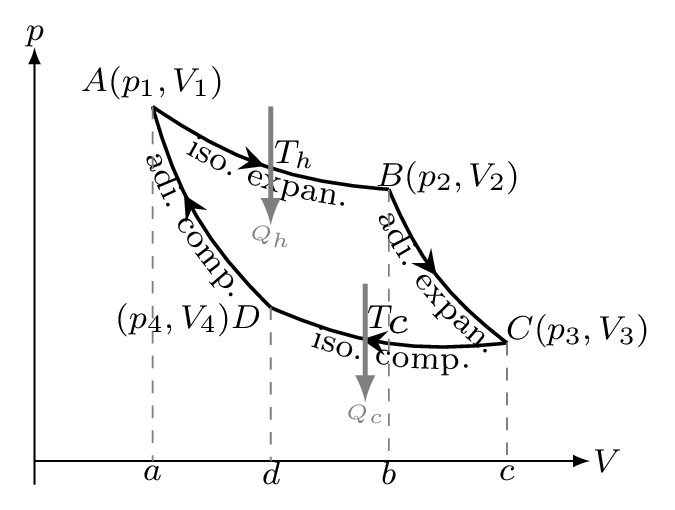
Step 1, Isothermal Expansion: Consider a mole of gas as a working substance in a cylinder [Figure 10.6.7]. The initial state of the gas is \((p_{1},V_{1})\) denoted by point A in the figure 10.25 and it’s temperature is the same as that of source \(T_{h}\, K\text{.}\) Let the cylinder be placed on the source and allowed to expand so slowly that the temperature remains constant at \(T_{h} \) throughout the expansion while \(Q_{h}\) amount of heat is being absorbed by the gas. The final state \((p_{2},V_{2})\) of the gas is represented by a point B. Because none of the heat goes into changing the temperature of the gas, all of the heat goes into pushing the piston up as the gas expands. Thus all of the heat, \(Q_{h}\) is turned into work, \(W_{1}.\) That is,
\begin{equation*}
Q_{h}=W_{1}=\int\limits^{v_{2}}_{v_{1}} p\,dV = RT_{h}\int\limits^{v_{2}}_{v_{1}} \frac{\,dV}{V}
\end{equation*}
\([pV=nRT,\quad n=1 \,mole]\)
\begin{equation*}
\therefore\quad W_{1} = RT_{h}\left[\log_{e}\right]^{v_{2}}_{v_{1}} = RT_{h}\log_{e}\frac{V_{2}}{V_{1}} =area ABba
\end{equation*}
Step 2, Adiabatic Expansion: Now the cylinder is removed from the source and placed on the stand. The gas is then allowed to expand adiabatically with no heat added to the system. The gas continues to expand, and the temperature of the gas drops to the temperature of the cold reservoir, \(T_{c},\text{.}\) If the volume of the gas has expanded, and the pressure is constant, then the temperature has to drop to compensate when reaches to a point \(C(p_{3},V_{3}).\)
The work done \(W_{2}\) in this case is given by
\begin{equation*}
W_{2} = \int\limits_{v_{2}}^{v_{3}}p\,dV = \int\limits_{v_{2}}^{v_{3}}k\frac{\,dV}{V^{\gamma}}
\end{equation*}
\([\because \quad pV^{\gamma}=constant, (k)]\) for adiabatic process.
\begin{equation*}
=k\left(\frac{V^{1-\gamma}}{1-\gamma}\right)_{v_{2}}^{v_{3}}
\end{equation*}
\begin{equation*}
=\frac{k}{1-\gamma} \left(V_{3}^{1-\gamma}-V_{2}^{1-\gamma}\right)
\end{equation*}
\begin{equation*}
= \frac{1}{1-\gamma} \left(p_{3}V_{3}^{\gamma}V_{3}^{1-\gamma}-p_{2}V_{2}^{\gamma}V_{2}^{1-\gamma}\right)
\end{equation*}
\([\because \quad p_{2}V_{2}^{\gamma}=p_{3}V_{3}^{\gamma}=k]\)
\begin{equation*}
\therefore\quad W_{2} = \frac{1}{1-\gamma}\left(p_{3}V_{3}-p_{2}V_{2}\right)
\end{equation*}
\begin{equation*}
=\frac{\left(RT_{c}-RT_{h}\right)}{1-\gamma}=\frac{R}{\gamma-1}\left(T_{h}-T_{c}\right) = area BCcb
\end{equation*}
Step 3, Isothermal compression: The cylinder is removed from stand and placed on the sink. The gas is then compressed slowly at constant temperature \(T_{c} \, K\) when the gas reaches to a point \(C(p_{4},V_{4}).\) The heat, \(Q_{c},\) is transferred to the cold reservoir by doing work \(W_{3}\) on it.
\begin{equation*}
\therefore\quad Q_{c} = W_{3} =-\int\limits_{v_{3}}^{v_{4}}p\,dV
\end{equation*}
\begin{equation*}
= -RT_{c}\int\limits_{v_{3}}^{v_{4}}\frac{\,dV}{V} =RT_{c}\log_{e}\frac{V_{3}}{V_{4}} =area DCcd
\end{equation*}
Step 4, Adiabatic compression: In the last step, the cylinder is removed from sink and placed once again on the stand. The gas is compressed adiabatically to the initial state \(A(p_{1}V_{1})\text{.}\) Since the heat can not be extracted from the gas as it causes the temperature of the gas to rise back to \(T_{h},\text{.}\) The work done on this compression is given by
\begin{equation*}
W_{4} = - \int\limits_{v_{4}}^{v_{1}}p\,dV = \frac{R\left(T_{h}-T_{c}\right)}{\gamma-1}=area ADda
\end{equation*}
Hence the total work done during the complete cycle of operation
\begin{equation*}
W=W_{1}+W_{2}+W_{3}+W_{4} = W_{1}-W_{3}
\end{equation*}
\([\because W_{2}=W_{4}] \)
Quantity of heat absorbed by the gas in full cycle \(= Q_{h}-Q_{c}=W_{1}-W_{3}\)
The efficiency of the Carnot cycle is therefore,
\begin{equation*}
\eta = \frac{\text{work done in cycle}}{\text{heat drawn from the source}}
\end{equation*}
\begin{equation*}
= \frac{W}{Q_{h}}= \frac{Q_{h}-Q_{c}}{Q_{h}} =1-\frac{Q_{c}}{Q_{h}}
\end{equation*}
Now,
\begin{equation*}
\frac{Q_{c}}{Q_{h}} = \frac{W_{3}}{W_{1}}
\end{equation*}
\begin{equation*}
= \frac{RT_{c}\log_{e}\frac{V_{3}}{V_{4}}}{RT_{h}\log_{e}\frac{V_{2}}{V_{1}}}
\end{equation*}
\begin{equation}
=\frac{T_{c}\log_{e}\frac{V_{3}}{V_{4}}}{T_{h}\log_{e}\frac{V_{2}}{V_{1}}}\tag{10.6.14}
\end{equation}
Since points B and C lie on the same adiabatic, we have -
\begin{equation*}
p_{2}V_{2}^{\gamma} = p_{3}V_{3}^{\gamma}
\end{equation*}
But,
\begin{equation*}
pV=RT \quad \Rightarrow\quad p=\frac{RT}{V}
\end{equation*}
\begin{equation*}
\therefore \quad T_{h}V_{2}^{\gamma-1} = T_{c}V_{3}^{\gamma-1}
\end{equation*}
\begin{equation}
\text{or,}\quad \frac{T_{c}}{T_{h}} = \left(\frac{V_{2}}{V_{3}}\right)^{\gamma-1} \tag{10.6.15}
\end{equation}
Similarly, points D and A lie on the same adiabatic, we have -
\begin{equation}
\text{or,}\quad \frac{T_{c}}{T_{h}} = \left(\frac{V_{1}}{V_{4}}\right)^{\gamma-1} \tag{10.6.16}
\end{equation}
\begin{equation*}
\left(\frac{V_{2}}{V_{3}}\right)^{\gamma-1} = \left(\frac{V_{1}}{V_{4}}\right)^{\gamma-1}
\end{equation*}
\begin{equation}
\frac{V_{1}}{V_{2}} = \frac{V_{4}}{V_{3}} \tag{10.6.17}
\end{equation}
\begin{equation*}
\frac{Q_{c}}{Q_{h}} = \frac{T_{c}\log_{e}\frac{V_{2}}{V_{1}}}{T_{h}\log_{e}\frac{V_{2}}{V_{1}}} = \frac{T_{c}}{T_{h}}
\end{equation*}
\begin{equation}
\therefore\quad \eta = 1-\frac{T_{c}}{T_{h}} \tag{10.6.18}
\end{equation}
This is the efficiency of Carnot’s heat engine. The Carnot’s engine can not be realized in practice because - (i) The temperature of source and sink can not be kept constant. The body (source) which loses energy its temperature falls gradually and the one (sink) which gains energy its temperature rises gradually, meaning reservoirs of infinite thermal capacity do not exist. (ii) It is a perfectly reversible in action, if the cycle is reversed the working substance will take \(Q_{c}\) amount of heat from sink and gives out \(Q_{h} \) amount of heat to the source, meaning reversible heat transfers are not possible. (iii) Heat transfer takes place at infinitesimally slow in isothermal process having very small temperature difference between the source and the receiver. On the other hand, in adiabatic process, heat transfer is zero and a very fast process.
