Subsection 3.3.2 Circular Kinematics
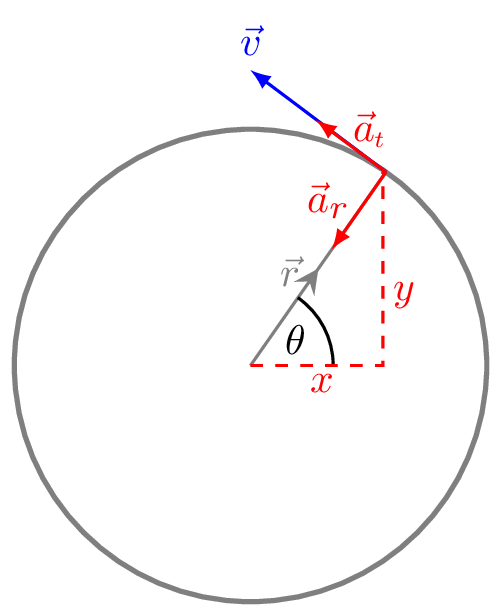
An object moving in a circular path is called a circular motion. In a uniform circular motion the direction of velocity is constantly changing but its magnitude remains constant. This constantly changing velocity vector produces the acceleration on an object which is pointed towards the center of a circle, called a centripetal acceleration. For this acceleration to happen there must exists a resultant force which is called the centripetal force. The centripetal force is not a physical force like frictional force, normal force, or gravity force, etc. it does not act on a body but it makes the body to rotate in a circle. This is a resulting force rather than a causing force like tension in a string, normal force acting on a body, frictional force between the surfaces of contact, and all fundamental forces. It is an unbalanced force. [Note that the causing force always comes in pair.] If \(r\) is the radius of the path, and \(T\) is the time period, the time it takes to complete a circle, then its speed (linear) is given by
\begin{equation*}
v = \frac{s}{t} = \frac{2\pi r}{T}
\end{equation*}
For a uniform circular motion centripetal acceleration \(a_{c} = a_{r}\text{,}\) is pointed along the radial direction towards its center and the tangential acceleration \(a_{t}\) is zero. For a non-uniform circular motion there is still a radial acceleration \(a_{c} = a_{r}\) but the tangential acceleration \(a_{t}\) is non-zero pointed along the direction of velocity. If the centripetal force vanishes, the object flies off at a tangent to the circle.
Subsubsection 3.3.2.1 Centripetal Acceleration:
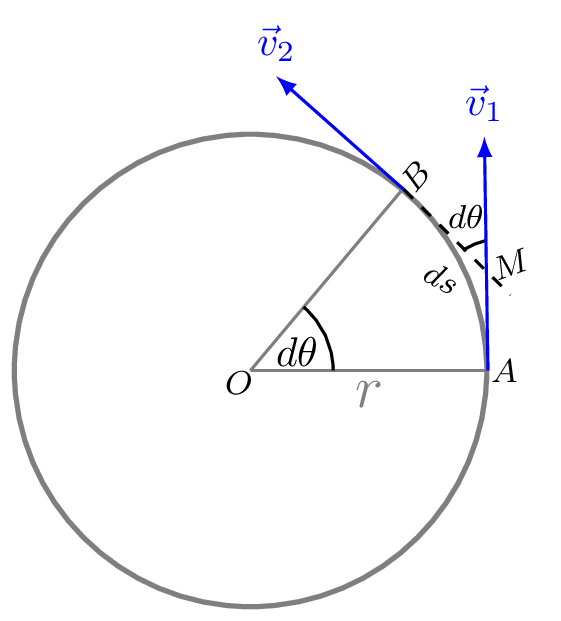
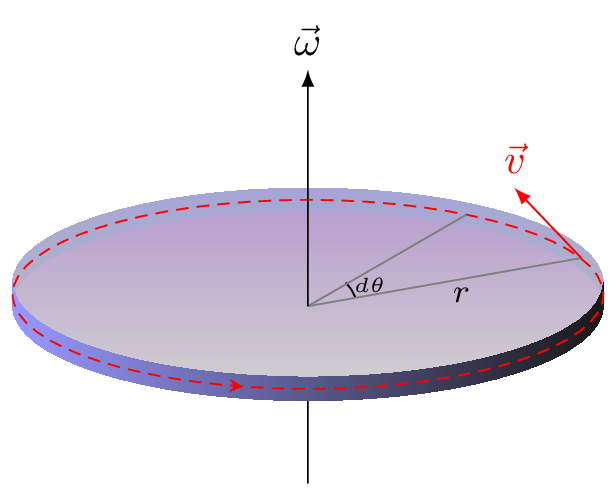
Consider a particle rotating in a circular path and reaches to point A from point B in a small time interval \(\,dt\text{.}\) The velocity vectors of the particle are \(\vec{v}_{1}\) at point A and \(\vec{v}_{2}\) at point B. The angular displacement subtends by the particle between point A and B is \(\,d\theta\) as shown in Figure 3.3.3.(a).
From quadrilateral OAMB of Figure 3.3.3.(a), \(\angle AOB+\angle AMB =180^{o}\) and \(\angle v_{1}AO+\angle MBO =180^{o}\) hence, \(\angle M = \,d\theta\) as \(\angle v_{1}MB = \angle v_{1}MA - \angle AMB \text{.}\) Now from radian formula,
\begin{equation*}
\,d\theta=\frac{\widehat{AB}}{r} = \frac{\,ds}{r}
\end{equation*}
Dividing both sides by \(\,dt\text{,}\) we get-
\begin{equation*}
\frac{\,d\theta}{\,dt} = \frac{1}{r}\frac{\,ds}{\,dt} \quad \Rightarrow \omega = \frac{v}{r}
\end{equation*}
\begin{equation}
\therefore\quad v=r\omega \tag{3.3.12}
\end{equation}
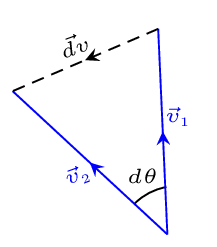
From Figure 3.3.3.(b), \(\vec{v}_{1}+\,d\vec{v}= \vec{v}_{2}\) also,
\begin{equation*}
\,d\theta = \frac{\,dv}{v}
\end{equation*}
Dividing both sides by \(\,dt\text{,}\) we get-
\begin{equation*}
\frac{\,d\theta}{\,dt} = \frac{1}{v}\frac{\,dv}{\,dt}
\end{equation*}
\begin{equation*}
\omega = \frac{a}{v} \quad \Rightarrow \quad a=v\omega
\end{equation*}
\begin{equation}
\therefore\quad a=\frac{v^{2}}{r}\tag{3.3.13}
\end{equation}
using eqn. (3.3.12) where \(a=a_{c}=\frac{v^{2}}{r}\text{,}\) is a centripetal acceleration. In uniform circular motion \(a_{c}=a_{r}\) is called the radial acceleration. In non-uniform circular motion the magnitude of a linear velocity is changing with time, and hence there is another acceleration presents along the tangential direction of motion, also called tangential acceleration. Which can be obtained by differentiating eqn.(3.3.12) w.r.t. ’t’,
\begin{equation*}
\frac{\,dv}{\,dt}=r\frac{\omega }{\,dt}
\end{equation*}
\begin{equation}
a_{t}=r\alpha \tag{3.3.14}
\end{equation}
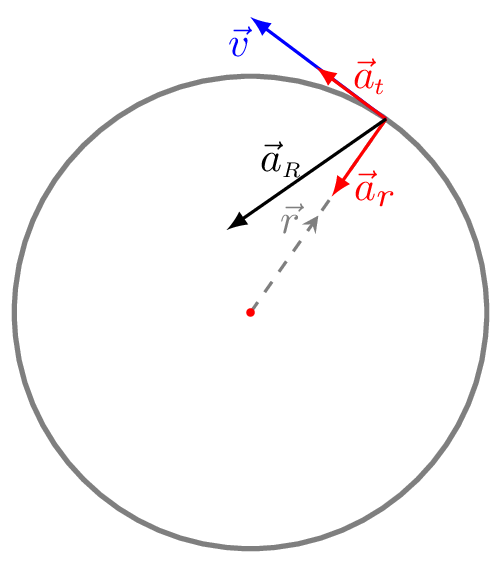
Hence the resultant acceleration in non-uniform circular motion [Figure 3.3.3.(c)] is given by
\begin{equation*}
a_{R}=\sqrt{a^{2}_{r}+a^{2}_{t}}
\end{equation*}
Subsubsection 3.3.2.2 Angular Displacement, \(\theta\text{:}\)
The angle subtends by an object when rotating in a circular path about an axis is called the angular displacement. In a 2D space, angular displacement describes a rotation of an object and is a simply number, a scalar. However, in 3D space, direction of the axis of rotation of an object need to be specified and hence it behaves as a vector. The direction of the vector is the direction of the axis of rotation, and the magnitude is how big the rotation was. Since angular displacement does not follow all the vectors rule in 2 dimension hence it is not taken as a vector quantity. For angular rotation in 2D,
\begin{equation*}
\vec{\theta_{1}}+\vec{\theta_{2}}\neq\vec{\theta_{2}}+\vec{\theta_{1}}\text{,}
\end{equation*}
i.e. not commutative for large angles. Suppose you have two pencils parallel to each other facing tips opposite to you. You rotate first pencil to \(90^{o}\) about vertical axis so that tip facing left side, then rotate it again by \(90^{o}\) about a horizontal axis so that its tip facing upward. Now rotate the second pencil by \(90^{o}\) about the horizontal axis so that its tip facing upward and again rotate it by \(90^{o}\) about a another horizontal axis so that tip facing left. Now you can see that they have different orientations, not parallel any more.
Subsubsection 3.3.2.3 Angular Velocity, \(\omega\text{:}\)
The angular velocity, \(\omega\) of an object is defined as the rate of change of angular displacement, \(\theta\text{.}\) That is, \(\omega=\frac{\theta}{t}\text{.}\) It is measured in unit (\(rad/s\)). It is a vector quantity and its direction is along the direction of axis of rotation defined by right hand thumb rule. If fingers of right hand are curled in the direction of rotation of the body then thumb pointed along the direction of angular velocity. The average angular velocity is given by
\begin{equation*}
\omega_{av} = \frac{\theta_{2}-\theta_{1}}{t_{2}-t_{1}}
\end{equation*}
and the instantaneous angular velocity is given by
\begin{equation*}
\omega = \frac{\,d\theta}{\,dt}.
\end{equation*}
Subsubsection 3.3.2.4 Angular Frequency, \(\omega\text{:}\)
It is also known as circular frequency which measures angular displacement per unit time. Its unit is therefore radians per second. It is a scalar quantity. It is related to angular velocity in the same way as circular motion is related to simple harmonic motion. If an object goes around a circle path once in a certain time T (in seconds), then it has subtended \(2\pi\) radians angle, and its angular velocity is thus \(\omega = \frac{\theta}{t}=\frac{2\pi}{t} \) radians per second. \(\frac{1}{T}=f\text{,}\) frequency and hence \(\omega=2\pi f,\) the angular frequency.
Subsubsection 3.3.2.5 Angular Acceleration, \(\alpha\text{:}\)
It is the rate of change of angular velocity. The average angular acceleration is given by
\begin{equation*}
\alpha_{av} = \frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}
\end{equation*}
and the instantaneous angular acceleration is given by
\begin{equation*}
\alpha = \frac{\,d\omega}{\,dt}.
\end{equation*}
Equations of motion in a circular motion:
\begin{equation}
\omega_{f}=\omega_{i}+\alpha t \tag{3.3.15}
\end{equation}
\begin{equation}
\omega^{2}_{f}=\omega^{2}_{i}+2\alpha\theta \tag{3.3.16}
\end{equation}
\begin{equation}
\theta = \omega_{i}t+\frac{1}{2}\alpha t^{2} \tag{3.3.17}
\end{equation}
