Subsection 6.1.5 Geosynchronous satellite
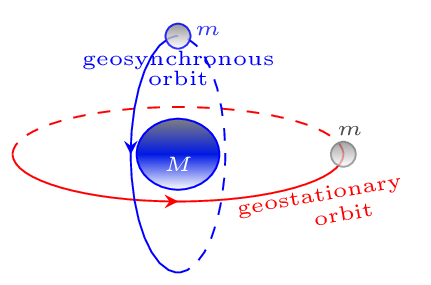
A geosynchronous satellite orbits the earth in such a way that it reaches at the same point above the earth in every 24 hours. It orbits in a polar orbit. The special kind of geosynchronous satellite is called geostationary satellite which seems to be at rest at the same position above the earth. It takes an equatorial orbit. The only force which provides the necessary centripetal force of such satellite is the gravitational force. Such satellites are used for weather forecasting and signal transmission.
\begin{equation}
F_{g}=\frac{GMm}{r^{2}} = \frac{mv^{2}_{o}}{r}\tag{6.1.1}
\end{equation}
Where \(m,\) \(v_{o},\) and \(r\) are mass, orbital velocity, and the orbital radius of the satellite, respectively. Also
\begin{equation}
v_{o} = \frac{2\pi r}{T} \tag{6.1.2}
\end{equation}
\begin{equation}
r =\sqrt[3]{\frac{GMT^{2}}{4\pi^{2}}}\tag{6.1.3}
\end{equation}
Since the angular speed of satellite in its orbit must be the same as that of the earth about its axis, the orbiting time period of satellite must be equal to 1 day. Therefore,
\begin{equation*}
T = 1 day = 24 h \times 60 \frac{min}{h}\times 60 \frac{sec}{min} = 86400 s
\end{equation*}
\begin{equation*}
\therefore \quad r=4.23\times10^{7} m
\end{equation*}
A geostationary satellite must orbit at a distance of about 36000 km above the surface of the earth, [\(\because\quad r=R+h\)].
