Section 2.1 Algebra of Vectors
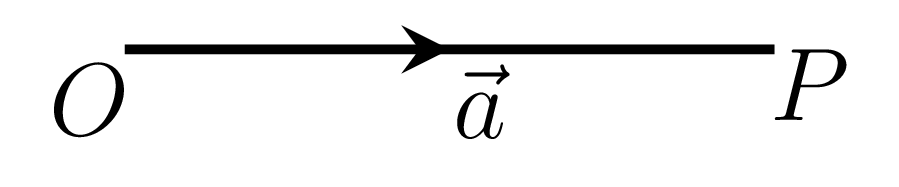
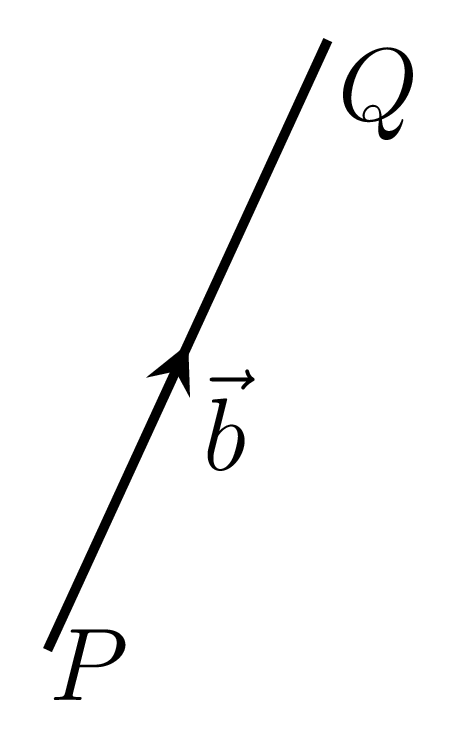
The mathematical operations of addition, subtraction, and multiplication in the algebra of numbers are also capable of getting extension in an algebra of vectors. A vector whose effect is same as that of a set of two vectors is called the resultant of the given vectors. Let \(\vec{OP} = \vec{a}\) and \(\vec{PQ} = \vec{b}\) are two vectors as shown in Figure 2.1.1.(a)–2.1.1.(b), then the resultant vector \(\vec{OQ} = \vec{r}\) is the sum of \(\vec{a}\) and \(\vec{b}\text{,}\) i.e., \(\vec{r}=\vec{a} + \vec{b}\) as shown in Figure 2.1.1.(c).
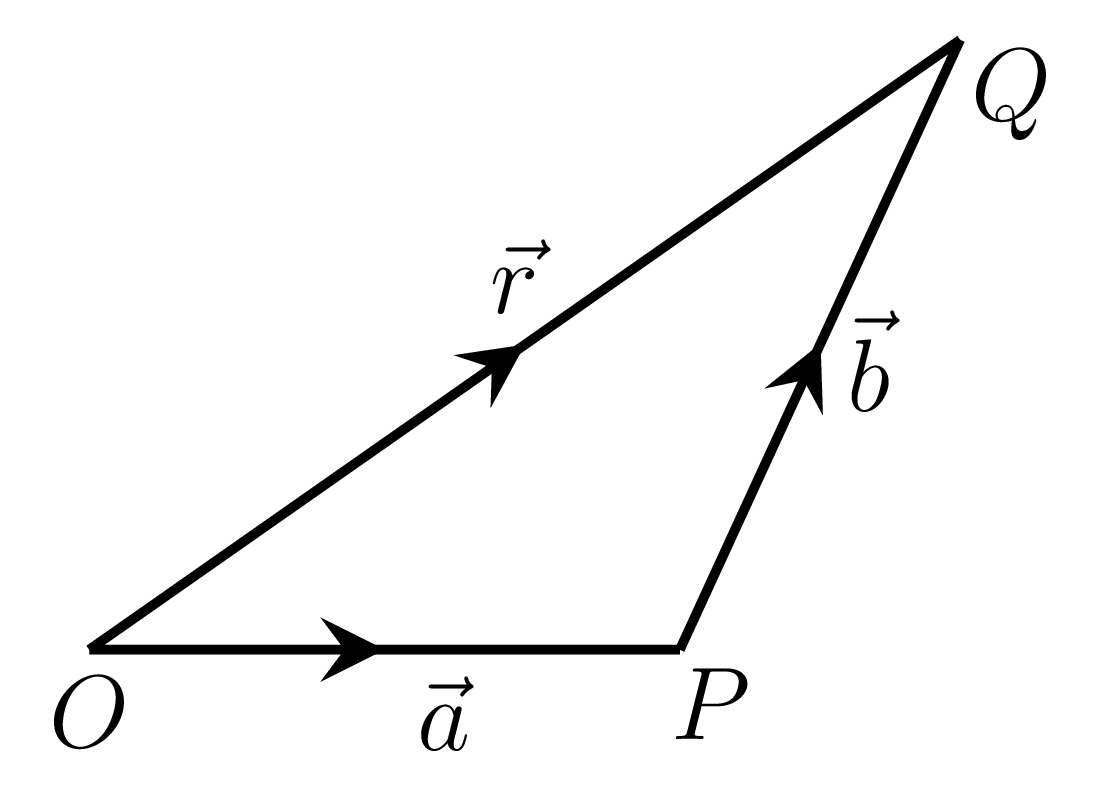
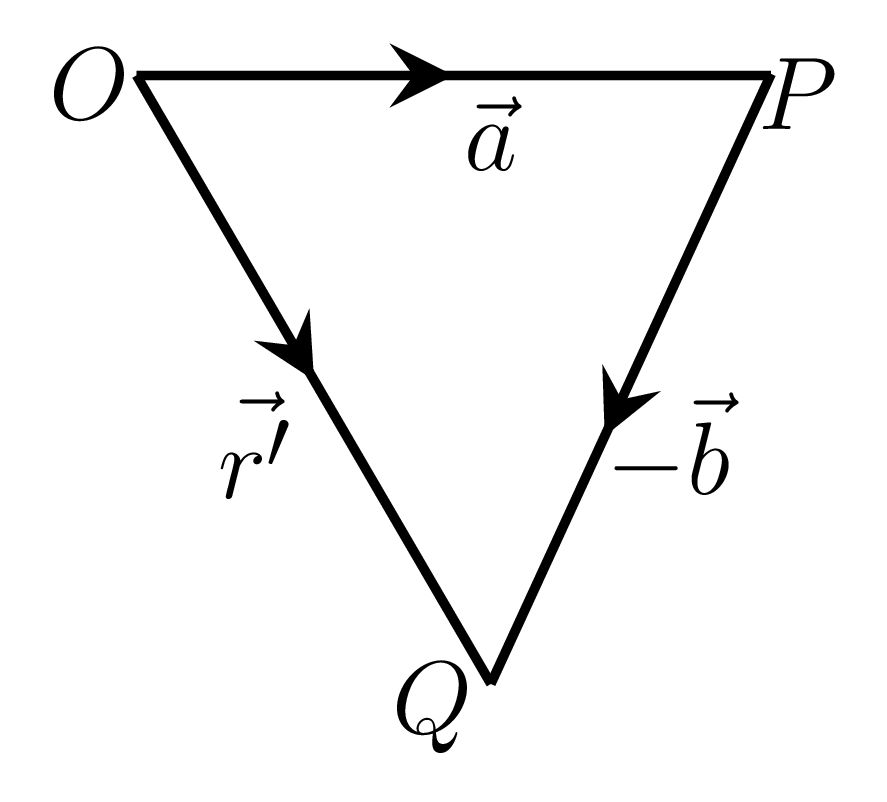
The resultant vector \(\vec{r'}\) or the subtraction of \(\vec{b}\) from \(\vec{a}\) is the addition of a negative vector of \(\vec{b}\) (i.e., \(-\vec{b}\)) to a \(\vec{a}\text{,}\) i.e.,
\begin{equation*}
\vec{r'} = \vec{a} - \vec{b} = \vec{a} + (-\vec{b})
\end{equation*}
as shown in Figure 2.1.1.(d). The resultant vector can be obtained by arranging the two individual vectors in such a way that the head of one vector falls onto the tail of another one without changing their individual directions. The resultant vector then joins the tail of first vector to the head of second vector (Remember the resultant vector is not in cyclic orientation of the individual vectors). If a vector \(\vec{a}\) is multiplied by any real positive number \(n\text{,}\) then the product \(n \vec{a}\) is a vector whose magnitude is \(n\) times as that of \(\vec{a}\) and its direction is the same as \(\vec{a}\text{.}\) If \(n\) is a negative number then the direction of \(n \vec{a}\) is opposite to \(\vec{a}\text{.}\) If \(\hat{a}\) is a unit vector in the direction of \(\vec{a}\) then, we have
- \(\vec{a} = |a| \hat{a},\) where \(|a|\) is a magnitude of \(\vec{a}\text{.}\)
- \((k+l)\vec{a} = (k+l)a \hat{a} = k a \hat{a} + l a \hat{a} = k \vec{a} + l \vec{a},\) where \(k\) and \(l\) are scalars.
- \(k(\vec{a} + \vec{b}) = k \vec{a} + k\vec{b}\text{.}\)
- \(k(l\vec{a}) = (k l) \vec{a}\text{.}\)
