Subsection 9.5.1 Capillary Action

Surface tension arises due to strong intermolecular forces of attraction between the molecules. When those forces act between like molecules, they are referred to as cohesive forces. Cohesion is a tendency of the liquid to remain as one assembly of particles. Surface tension is due to cohesion between particles at the free surface. A liquid, however, is often in contact with a solid surface, such as glass. Hence the additional forces of attraction occur between molecules of the liquid and molecules of the solid surface. When the attractive forces act between unlike molecules, they are said to be adhesive forces. This property enables a liquid to stick to another body.
Capillary is a phenomenon by which a liquid rises up into a narrow tube (called capillary) above or below its general level. The upper surface of a liquid in a tube is called the meniscus, and the shape of the meniscus depends on the relative strengths of the cohesive and adhesive forces. In liquids such as water, the meniscus is concave, because of high adhesive forces between water and glass molecules. In liquids such as mercury, the meniscus is convex because the molecules of mercury have very strong cohesive forces and weak adhesion to glass. The height to which the water rises depends on the diameter of the tube and the temperature of the water but not on the angle of tilt of the tube in water. The smaller the diameter, the higher the liquid rises.
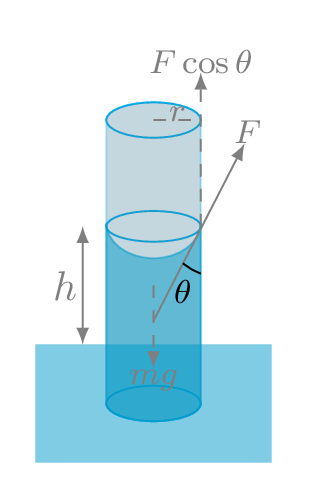


Capillary action provides wetting ability of liquids on the solid interfaces. The contact angle \(\theta\) between the liquid boundary and the solid surface is a measure of the degree of wetting. Adhesion and surface tension together can produce capillary action. Capillary action occurs when the adhesion to the walls is stronger than the cohesive forces between the liquid molecules. Adhesion of water to the walls of a vessel results in an upward force on the liquid at the edges. The water keep rising in the capillary till the weight of this portion of water is balanced by the vertical component of such upward force. From Figure 9.5.3.(a), we have -
\begin{equation*}
mg=F\cos\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad V\rho g = \gamma l \cos\theta
\end{equation*}
\([\because F=\gamma l, \quad m=V\rho]\)
\begin{equation*}
\text{or,}\quad (\pi r^{2}h)\rho g = \gamma (2\pi r) \cos\theta
\end{equation*}
\([\because V=area\times height, \quad l=2\pi r]\) Here \(\rho\) is density of liquid like water, \(r\) is radius of capillary, and \(\theta\) is angle of contact.
\begin{equation*}
\therefore \quad h = \frac{2\gamma\cos\theta}{\rho r g}
\end{equation*}
A smaller contact angle and a smaller surface tension result in a greater the degree of wetting. When adhesive forces are greater than cohesive forces, the contact angle \(\theta\) lies between 0 and \(90^{o}.\) When adhesive forces are smaller than cohesive forces, the contact angle \(\theta\) lies between \(90^{o}\) and \(180^{o}\) [Figure 9.5.3.(b) and Figure 9.5.3.(c)]. When water is dripping from the narrow orifice its shape is a little bit oval because of gravity. However, the shape would be completely spherical in absence of gravity because of surface tension of the water.
