Heat Transfer

Subsection 10.3.6 Heat Transfer

It is process by which heat transfers from one location to another due to temperature difference. Heat can only flow from high temperature to low temperature. There are three processes involved in heat transfer. They are conduction, convection, and radiation.

Conduction.
In this process heat is transferred through stationary matter by physical contact. In microscopic level atoms and molecules are always in random motion at any temperature above absolute zero. When heated these particles (atoms and molecules) gain thermal energy and begin vibrating even higher amplitude knocking the neighboring particles. By doing so they impart some of their energy to their neighboring particles, and so on. Eventually heat is carried away from one end of a substance to another. In conduction, heat carrying particles do not physically move from its place rather they transfer their energy to neighbors when they knock one another. Every time they knock pass some of their energy to next one and returns to their original place. Heat transfers from the burner of a stove through the bottom of a pan to food in the pan is transferred by conduction. Conduction occurs in all states of substances solid, liquid, and gas. In solids, conduction happens due to molecular vibration. In gases and liquids, it is due to collisions and diffusion of the molecules during their random motion.

Consider one end of a metallic bar [Figure 10.3.4] of length \(l\) and area of cross-section \(A\) is kept at hot temperature \(T_{h}^{o}C\) and another end is kept at cold temperature \(T_{c}^{o}C\text{,}\) then the amount of heat, \(Q\) transfers through this bar at time \(t\) can be found experimentally as

\begin{equation} Q \propto A \tag{10.3.1} \end{equation}

\begin{equation} Q \propto \Delta T \tag{10.3.2} \end{equation}

\begin{equation} Q \propto \frac{1}{l}\tag{10.3.3} \end{equation}

\begin{equation} Q \propto t \tag{10.3.4} \end{equation}

combining these all, we get -

\begin{equation*} Hence,\quad Q \propto \frac{A \Delta T t}{l} \end{equation*}

\begin{equation} \therefore \quad Q =\frac{\kappa A t \Delta T }{l} =\frac{\kappa A t \left(T_{h}-T_{c}\right) }{l} \tag{10.3.5} \end{equation}

where \(\kappa\) is a proportionality constant, known as coefficient of thermal conduction or conductivity of a material. It is a material property.

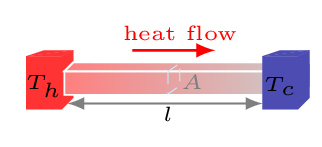
Figure 10.3.4.

In differential form,

\begin{equation*} \frac{\,dQ}{\,dt}=\kappa A \frac{\,dT}{\,dx} \end{equation*}

where \(\,dx\) is a length of the bar. That is, the rate of heat flow at any point is proportional to the temperature gradient (how fast the temperature is changing with position).

\begin{equation*} \frac{\,dQ}{\,dt}\propto \frac{\,dT}{\,dx} \end{equation*}

The ratio of thickness to the conductivity of a material can be known as R-values. Hence,

\begin{equation*} R_{i} = \frac{l_{i}}{k_{i}} \end{equation*}

and the rate of heat flow can be given by

\begin{equation*} H =\frac{Q}{t} = \frac{A \Delta T}{\sum R_{i}} \end{equation*}
Convection.
In this process heat transfer occurs by the actual movement of fluid particles. Convection heat transfer is energy transport due to bulk fluid motion. Convection happens in gases and liquids.

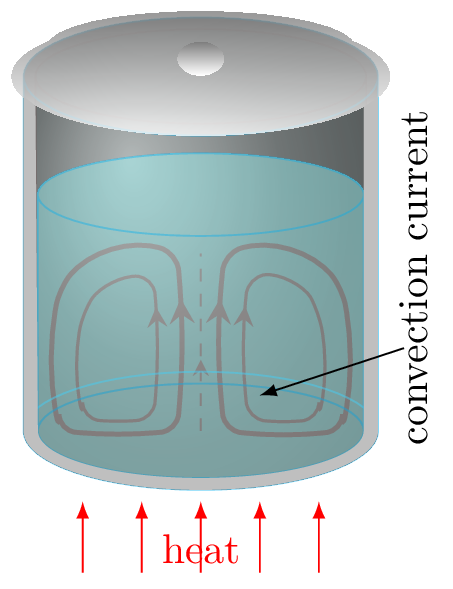
Figure 10.3.5.

When a fluid is heated, its molecules which are in contact with the hot surface get hot and expand. That is, the fluid above a hot surface expands, becomes less dense, and rises. It carries the thermal energy along when rises up. The relatively cold fluid on the upper surface is heavier and sink down near the heat source. Hence a current of heat cycle develops in the convection process, called convection cycle. The rate of heat flow in convection process is given by

\begin{equation} H=\frac{Q}{t}=hA(T_{s}-T_{f})\tag{10.3.6} \end{equation}

where \(h\) is known as convective heat transfer coefficient, \(A\) is surface area of fluid receiving heat, \(T_{s},\) and \(T_{\infty}\) are temperature of hot surface and cold fluid, respectively. The unit of \(h\) is \(W/m^{2}.\,^{o}C.\)
Radiation.

It is the process in which heat transfer without the need of intervening medium. Heat transfer occurs in this process when electromagnetic waves emitted or absorbed. The warming of the earth surface by the Sun is due to radiation. Heat transfer by this process is the fastest one. All bodies above absolute zero emit thermal radiation. At room temperature the radiation is in the infrared range, wavelengths longer than those of the visible spectrum. In atomic domain, the radiation is caused because of oscillating ions and electrons in a warm solid are accelerating electric charges, such charges radiate. Different substances radiate with different efficiencies. The good radiator of radiation is a good absorber of radiation. A perfect absorber is called a black body (such perfection is not found in nature, but some things are close). Hence a black body is also a perfect radiator. A black body absorbs and emits radiation of all most all frequencies. It was found experimentally that heat energy radiated per unit time per unit surface area of a perfectly black body is proportional to the fourth power of its absolute temperature. This statement is also called Stefan-Boltzmann law. That is,

\begin{equation*} \frac{E}{tA}\propto T^{4} \end{equation*}

\begin{equation} \therefore \quad P = \sigma A \epsilon T^{4}\tag{10.3.7} \end{equation}

where \(\sigma = 5.67\times10^{-8} \,W/m^{2}.K^{4}\) is called Stefan-Boltzmann constant and \(\epsilon\) is called emissivity of the object. For a perfect black body \(\epsilon=1.\) If \(T\) and \(T_{o} \) be the temperatures of the body and its surroundings then, net rate of heat loss,

\begin{equation*} P=\sigma A \epsilon \left(T^{4}-T_{o}^{4}\right) \end{equation*}

For any particular wavelength and temperature the amount of thermal radiation emitted depends on the emissivity of the object’s surface. Emissivity is defined as the ratio of the energy radiated from a material’s surface to that radiated from a blackbody at the same temperature and wavelength under the same viewing conditions. It is a dimensionless number between 0 (for a perfect reflector) and 1 (for a perfect emitter). The emissivity of a surface depends not only on the material but also on the nature of the surface. For example, a clean and polished metal surface will have a low emissivity, whereas a roughened and oxidized metal surface will have a high emissivity. The emissivity also depends on the temperature of the surface as well as wavelength and angle.

To calculate temperature, heat transfer, and energy balance in various systems or to understand the transfer of energy (heat) as electromagnetic radiation between objects the following terminologies are very important to know.

Emissive Power.
It is defined as the radiant energy emitted per unit time per unit surface area of the body at a particular temperature within a unit wavelength range. Emissive power represents the rate at which an object emits electromagnetic radiation, typically in the form of thermal radiation (infrared radiation) due to its temperature. Emissive power depends on the temperature of the object and its emissivity. Emissivity is a material property that describes how efficiently an object can emit radiation compared to an ideal black body, which has an emissivity of 1. Objects with higher emissivity values emit radiation more effectively.
Absorptive Power.
It is defined as the ratio of radiant energy absorbed per unit time per unit surface area of the body to the total energy falling per unit time on the same area at a particular temperature within a unit wavelength range. Absorptive power represents the ability of an object to absorb electromagnetic radiation. It is the complement of reflectivity and is related to how efficiently a material can absorb incoming radiation. Materials with high absorptivity values absorb more radiation and convert it into thermal energy. Absorptivity, like emissivity, is also a material property and varies with wavelength. It is a unitless value between 0 and 1.
Kirchhoff’s Law.
Kirchhoff has two fundamental principles in the study of thermal radiation and the behavior of materials with regard to electromagnetic radiation. The details of Kirchhoff’s law is not a part of discussion here but only taken here for some information. Kirchhoff’s first law states that at any temperature, the ratio of the emissive power to the absorptive power for a given wavelength is the same for all bodies and is equal to the emissive power of a perfectly black body.

In other words, this law states that the emissivity (\(\epsilon\)) of an object at a particular wavelength is equal to its absorptivity (\(\alpha\)) at that same wavelength. That is,

\begin{equation*} \epsilon (\lambda) = \alpha(\lambda) \end{equation*}

the amount of radiation that an object emits at a specific wavelength is equal to the amount of radiation it absorbs at that same wavelength when the object is in thermal equilibrium with its surroundings.

Kirchhoff’s second law states that at every temperature and for every wavelength, the emissivity (\(\epsilon\)) of a perfect black body is equal to 1. That is,

\begin{equation*} \epsilon (\lambda) =1 \end{equation*}

a perfect black body is an idealized object that absorbs all incident radiation and emits radiation at the maximum possible rate for a given temperature. It is often used as a reference to compare the behavior of real objects in radiative heat transfer.

Prev Top Next