Subsection 9.4.3 Stoke’s Law
The viscous force acting on a small spherical body moving through a fluid is directly proportional to viscosity, \(\eta,\) of the fluid, radius \(r\) of the body, and its velocity, \(v.\) That is,
\begin{equation*}
F\propto r^{a}v^{b}\eta^{c}
\end{equation*}
Using dimensional analysis, we have
\begin{equation*}
F = kr^{a}v^{b}\eta^{c}
\end{equation*}
\begin{equation*}
\text{or,}\quad [MLT^{-2}] = k [L]^{a}[LT^{-1}]^{b}[ML^{-1}T^{-1}]^{c} =k [M]^{c}[L]^{a+b-c}[T]^{-b-c}
\end{equation*}
From the principle of homogeneity,
\begin{equation}
c=1 \tag{9.4.6}
\end{equation}
\begin{equation}
-b-c = -2 \quad \Rightarrow\quad b=1 \tag{9.4.7}
\end{equation}
\begin{equation}
a+b-c =1 \quad \Rightarrow\quad a=1 \tag{9.4.8}
\end{equation}
\begin{equation*}
\therefore\quad F = k\eta r v
\end{equation*}
From experiment, \(k=6\pi\text{,}\) Therefore
\begin{equation}
F = 6\pi \eta r v \tag{9.4.9}
\end{equation}
Which is a stoke’s equation.
Subsubsection 9.4.3.1 Terminal velocity of a body moving through a fluid
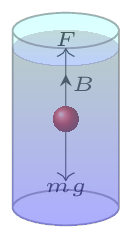
As the body falls through a medium, its velocity goes on increasing due to gravity. As the viscous force is velocity dependent, it also goes on goes on increasing till it reaches a constant velocity called terminal velocity. This happen when the weight of the body is just equal to the sum of the upward thrust due to buoyancy and the upward viscous drag. At this stage, there is no net force to accelerate the body. Let \(\rho \) be the density of the material of the spherical body of radius r and \(\sigma\) be the density of the medium. Hence,
\begin{equation*}
F+B=W
\end{equation*}
where F is viscous drag force, B is bouyant force, and W is weight of the body.
\begin{equation*}
6\eta r v + V\sigma g = V\rho g
\end{equation*}
\begin{equation*}
\text{or,}\quad 6\eta r v = V(\rho-\sigma) g =\frac{4}{3}\pi r^{3}(\rho-\sigma) g
\end{equation*}
\begin{equation*}
\therefore\quad v= \frac{2r^{2}(\rho-\sigma) g}{9\eta}
\end{equation*}
The initial acceleration, \(a\) of the body can be found by using the concept of Archimedes principle.
The apparent weight of the body = weight of the body in air - buoyant force.
\begin{equation*}
W' = W-B
\end{equation*}
\begin{equation*}
\text{or,}\quad ma = mg - V\sigma g
\end{equation*}
\begin{equation*}
\text{or,}\quad a = g - \frac{V}{m}\sigma g
\end{equation*}
\begin{equation*}
\text{or,}\quad a = \left(1-\frac{V\sigma}{V\rho}\right)g
\end{equation*}
\begin{equation*}
\therefore\quad a= \left(1-\frac{\sigma}{\rho}\right)g
\end{equation*}
