Subsection 10.5.1 Pressure of an Ideal Gas
When the molecules of a gas collide on the walls of the container (or each other) they exert a pressure. Let us consider a cube of sides \(l\) cm encloses \(N\) number of molecules and mass of each molecule is \(m\text{.}\) Since time during the collision of molecules is so small there is no transfer of momentum hence no exertion of force (Newton’s II law) or no pressure, we ignore therefore the collision of molecules amongst themselves here. Let a molecule at point \(p\) is moving with velocity \(\vec{v}\) in any direction. This velocity can be resolved into x,y, and z directions as \(v_{x}, \quad v_{y}, \) and \(v_{z},\) respectively, such that
\begin{equation}
v^{2}=v^{2}_{x}+v^{2}_{y}+v^{2}_{z} \tag{10.5.1}
\end{equation}
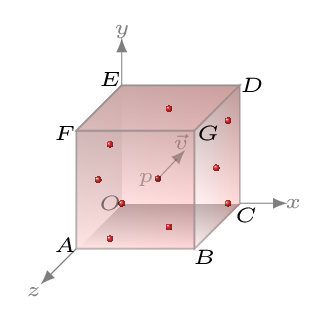
Let a molecule collide elastically on the face BCDG along x-axis [Figure 10.5.1]. The momentum of the molecule along x-axis before collision is \(mv_{x}.\) Since the collision is elastic the molecule rebound with the same velocity along opposite to x-axis. Therefore the momentum in this case will be \(-mv_{x}.\) The change in momentum of the molecule due to this collision along x-axis will be
\begin{equation*}
\Delta p = mv_{x} -(-mv_{x})= 2mv_{x}.
\end{equation*}
Now once this molecule collide to the face EFAO while moving along -ve axis and rebounds it again comes to collide with the same face BCDG. The distance traveled by the molecule for collision on the same face is \(2l.\) Hence, the time taken between each successive collision on face BCDG is given by
\begin{equation*}
\Delta t=\frac{d}{v}=\frac{2l}{v_{x}}
\end{equation*}
Therefore, the force exerted on the face BCDG by molecule \(l\) is given by Newton’s II law of motion,
\begin{equation*}
f_{x_{1}}=\frac{\Delta p}{\Delta t} = \frac{(2mv_{x_{1}})v_{x_{1}}}{2l}=\frac{mv^{2}_{x_{1}}}{l}
\end{equation*}
Since there are \(N\) molecules hence total force exerted on the face BCDG is given by
\begin{equation*}
f_{x} = f_{x_{1}} +f_{x_{2}}+f_{x_{3}}+\cdots
\end{equation*}
\begin{equation*}
= \frac{m}{l}\left(v^{2}_{x_{1}}+ v^{2}_{x_{2}}+v^{2}_{x_{3}}+\cdots +v^{2}_{x_{N}}\right)
\end{equation*}
The pressure on the face BCDG will be
\begin{equation*}
p_{x} = \frac{F}{A}
\end{equation*}
\begin{equation*}
= \frac{f_{x}}{l^{2}}=\frac{m}{l^{3}}\left[\sum\limits_{i=1}^{N}v^{2}_{x_{i}}\right]
\end{equation*}
Similarly, pressures \(p_{y},\) and \(p_{z}\) along the y- and z- axes, respectively are
\begin{equation*}
p_{y} =\frac{m}{l^{3}}\left[\sum\limits_{i=1}^{N}v^{2}_{y_{i}}\right]
\end{equation*}
and
\begin{equation*}
p_{z} =\frac{m}{l^{3}}\left[\sum\limits_{i=1}^{N}v^{2}_{z_{i}}\right]
\end{equation*}
Hence, the average pressure in the container
\begin{equation*}
p=\frac{p_{x}+p_{y}+p_{z}}{3}
\end{equation*}
\begin{equation*}
=\frac{m}{3l^{3}}\left[\sum\limits_{i=1}^{N}\left(v^{2}_{x_{i}}+v^{2}_{y_{i}}+v^{2}_{z_{i}}\right)\right]
\end{equation*}
\begin{equation*}
p=\frac{m}{3l^{3}}\left[\left(v^{2}_{x_{1}}+v^{2}_{y_{1}}+v^{2}_{z_{1}}\right)+\left(v^{2}_{x_{2}}+v^{2}_{y_{2}}+v^{2}_{z_{2}}\right)+\cdots+ \left(v^{2}_{x_{N}}+v^{2}_{y_{N}}+v^{2}_{z_{N}}\right)\right]
\end{equation*}
\begin{equation*}
p=\frac{m}{3l^{3}}\left[v^{2}_{1}+v^{2}_{2}+\cdots+v^{2}_{N}\right] =\frac{m}{3V}N\overline{v^{2}}
\end{equation*}
\begin{equation}
\therefore\quad p=\frac{1}{3}\left(\frac{M}{V}\right)\overline{v^{2}} \tag{10.5.2}
\end{equation}
where
\begin{equation*}
\overline{v^{2}} = \left[\frac{v^{2}_{1}+v^{2}_{2}+\cdots+v^{2}_{N}}{N}\right]
\end{equation*}
and
\begin{equation}
\overline{v}=\sqrt{\frac{v^{2}_{1}+v^{2}_{2}+\cdots+v^{2}_{N}}{N}}\tag{10.5.3}
\end{equation}
Here, \(\overline{v} =v_{rms}\) is called a root-mean square velocity of the molecule and is an average molecular speed and \(mN=M,\) the mass of total gas in a container of volume \(V.\)
\begin{equation}
\therefore\quad p=\frac{1}{3}\rho \overline{v^{2}} \tag{10.5.4}
\end{equation}
\begin{equation*}
\text{or,}\quad pV=\frac{1}{3}M\overline{v^{2}}=\frac{2}{3}\cdot\frac{1}{2}M\overline{v^{2}}
\end{equation*}
\begin{equation}
\text{or,}\quad pV = \frac{2}{3}KE \tag{10.5.5}
\end{equation}
where \(\frac{1}{2}M\overline{v^{2}}\) = average transational kinetic energy of the gas and \(\frac{1}{2}m\overline{v^{2}} = \overline{e_{k}},\) is the average transational kinetic energy of each moleucle.
\begin{equation*}
\therefore\quad p=\frac{2}{3}\frac{KE}{V}
\end{equation*}
That is, pressure is two-thirds of the total transational kinetic energy of the molecules per unit volume. Now from postulates average kinetic energy of the molecules of the gas depends only on temperature, we have
\begin{equation*}
\overline{e_{k}}\propto T
\end{equation*}
\begin{equation}
\text{or,}\quad \frac{1}{2}m\overline{v^{2}} = \frac{f}{2}k_{B}T =\frac{3}{2}k_{B}T \tag{10.5.6}
\end{equation}
where \(f\) is a degree of freedom for a gas molecules and \(k_{B}\) is called the Boltzmann constant. In SI system, \(k_{B} = 1.380\times10^{-23} \,J/K.\)
