Subsection 9.2.1 Equation of Continuity
As a fluid is in steady motion and its flow progresses with time, it must be that the amount of mass flowing per unit time across to areas perpendicular to the flow is conserved. The flow rate is a measure of the flow of mass (volume) of fluid per unit time.
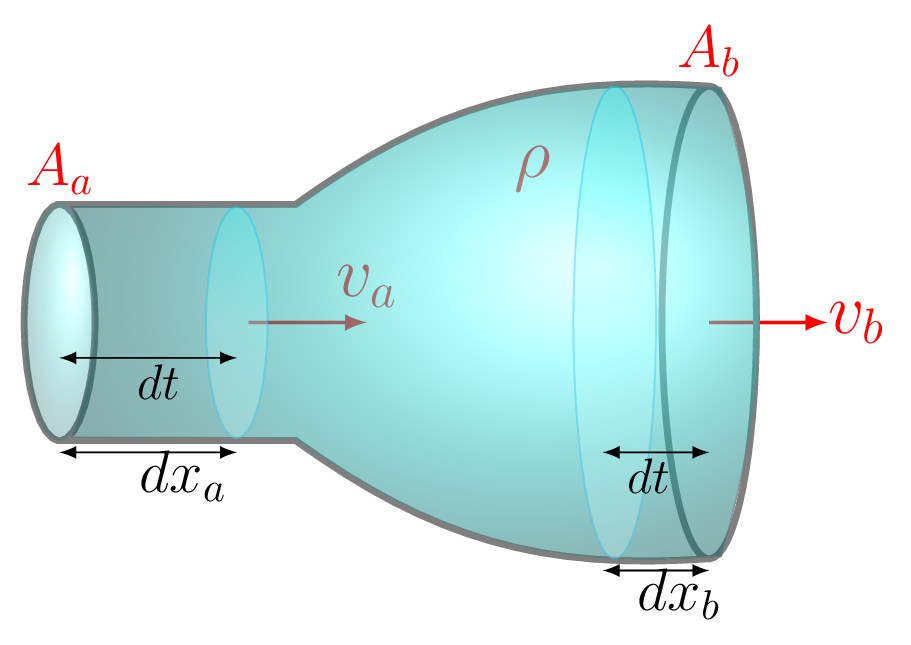
Consider a tube [Figure 9.2.1] with areas of cross-section \(A_a\) at one end and \(A_b\) at another end. If \(\,dm\) mass of fluid is entering into the tube in time \(\,dt\) then the same amount of fluid must be leaving out of the tube in the same interval of time because fluid is incompressible. Hence, flow rate of fluid in laminar flow is same throughout its path, i.e.,
\begin{equation*}
\left.\frac{\,dm}{\,dt}\right]_{a} =\left.\frac{\,dm}{\,dt}\right]_{b}
\end{equation*}
\begin{equation*}
\text{or,}\quad \rho_{a}\frac{\,dV_{a}}{\,dt} =\rho_{b}\frac{\,dV_{b}}{\,dt}
\end{equation*}
\begin{equation*}
\text{or,}\quad \rho A_{a}\frac{\,dx_{a}}{\,dt} =\rho A_{b}\frac{\,dx_{b}}{\,dt}
\end{equation*}
\(\because \rho_{a}=\rho_{b}=\rho]\)
\begin{equation}
\therefore\quad A_{a} v_{a} = A_{b} v_{b} = constant \tag{9.2.1}
\end{equation}
The quantity \(Av\) is called a flow rate. This equation is called an equation of continuity.
