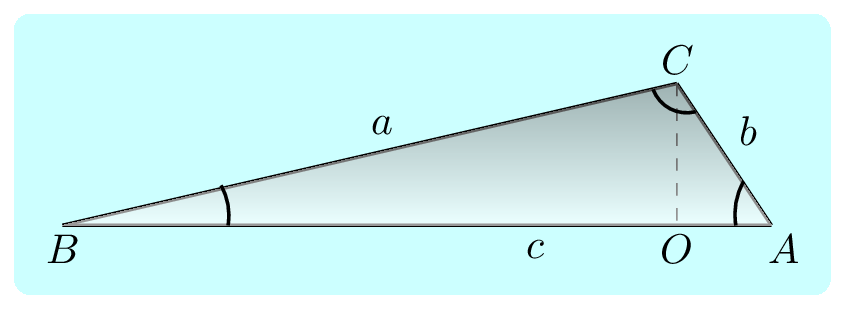
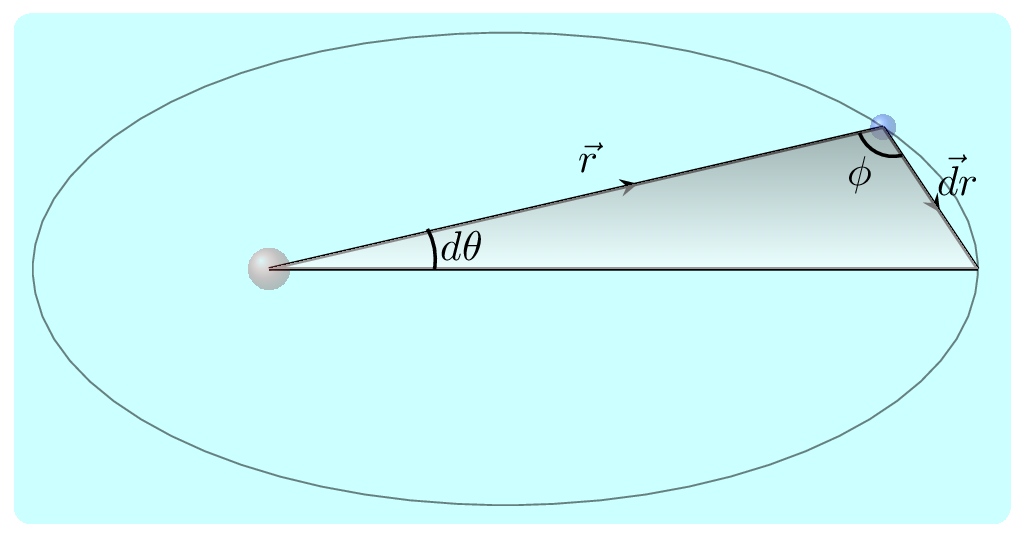
The small area of a given triangle
\begin{align*}
\,dA \amp = \frac{1}{2}r\,dr\sin\phi \\
or, \quad \,d\vec{A} \amp = \frac{1}{2}(\vec{r} \times \,d\vec{r}) \\
or, \quad \frac{\,d \vec{A}}{\,dt} \amp = \frac{1}{2}[\vec{r} \times \frac{\,d\vec{r}}{\,dt}]
\end{align*}
\begin{equation}
or, \quad \frac{\,d\vec{A}}{\,dt} = \frac{1}{2}[\vec{r} \times \vec{v}] \tag{6.2.30}
\end{equation}
But from angular momentum, we have
\begin{equation*}
\vec{L}=m(\vec{r}\times\vec{v})
\end{equation*}
\begin{equation*}
\frac{\,d\vec{A}}{\,dt} = \frac{\vec{L}}{2m}
\end{equation*}
and
\begin{align*}
or, \quad \vec{\dot{A}} \amp = \frac{1}{2m}\vec{L} = \frac{1}{2}[\vec{r}\times (\dot{r}\hat{r}+r\dot{\theta}\hat{\theta})] \\
\amp = \frac{1}{2}[r\hat{r}\times r\dot{\theta}\hat{\theta}] = \frac{1}{2}[r\hat{r}\times (\frac{Lr}{mr^2})\hat{\theta}] \\
\amp = \frac{L}{2m}[\hat{r}\times \hat{\theta}] = \frac{L}{2m} \hat{n}
\end{align*}
by using
(6.2.4) and
(6.2.9). Also
\(\vec{r}\times \hat{r} =0\) and
\(\hat{n}\) is a unit vector perpendicular to the plane of orbit. Again,
\begin{equation*}
\vec{\ddot{A}} = \frac{\,d}{\,dt}(\vec{\dot{A}}) = \frac{\,d}{\,dt}[\frac{L}{2m}] = 0
\end{equation*}
\begin{equation}
\vec{\dot{A}} = \frac{\,d\vec{A}}{\,dt} = constant.\tag{6.2.31}
\end{equation}
That is areal velocity of planet is constant.