Subsection 3.1.1 Analyzing the motion curve
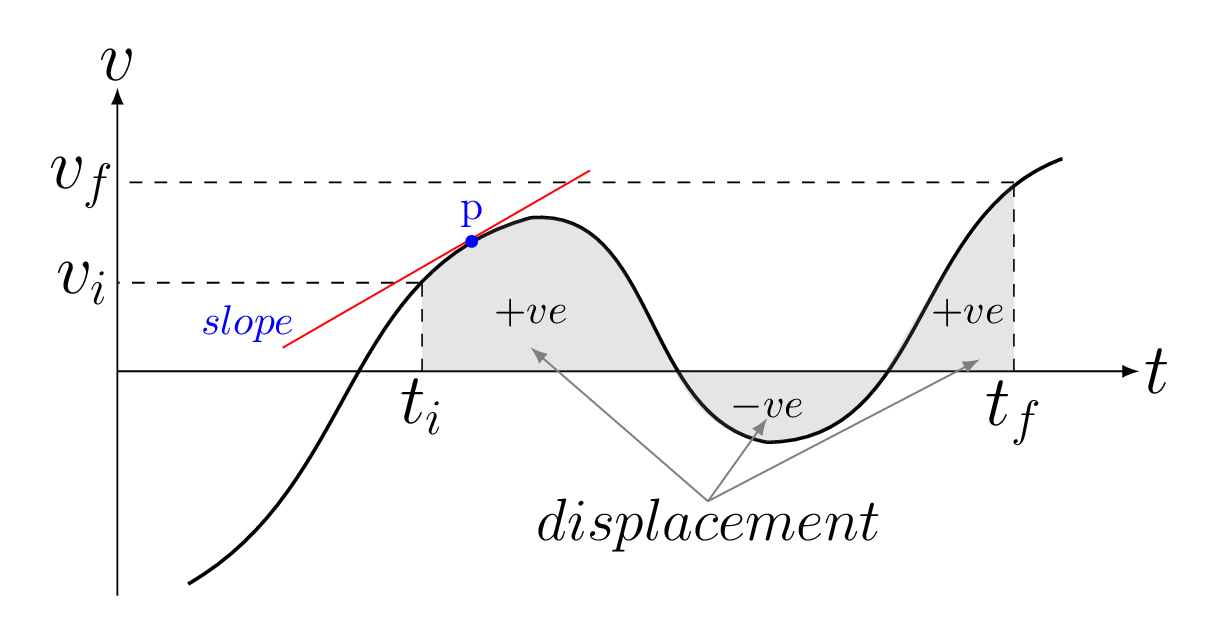
The slope in \(v\) vs. \(t\) graph gives instantaneous acceleration and the area between the velocity curve and the time axis gives the displacement. Acceleration relates to velocity in \(v \sim t\) graph in the same manner as velocity relates to position in \(x \sim t\) graph Figure 3.1.7. Curvature in position-time graph gives the instantaneous acceleration. Since the slope of the velocity curve, \(\frac{\,dv}{\,dt}\text{,}\) is the time rate of change of velocity, or \(\frac{\,d^{2}x}{\,dt^{2}}\) which is called the bending function of the position-time curve.
Subsubsection 3.1.1.1 Reading of \(x \sim t\) graph
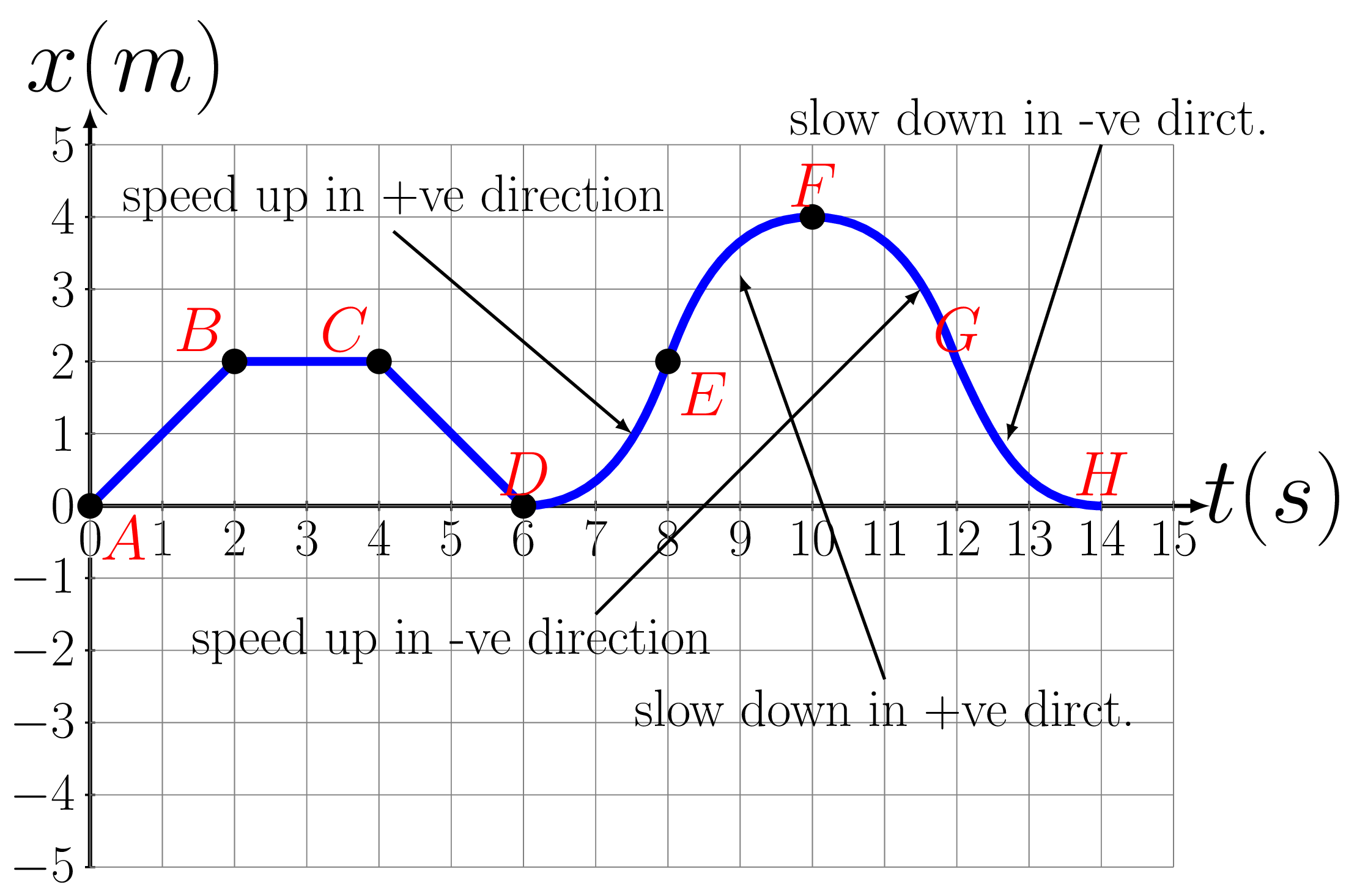
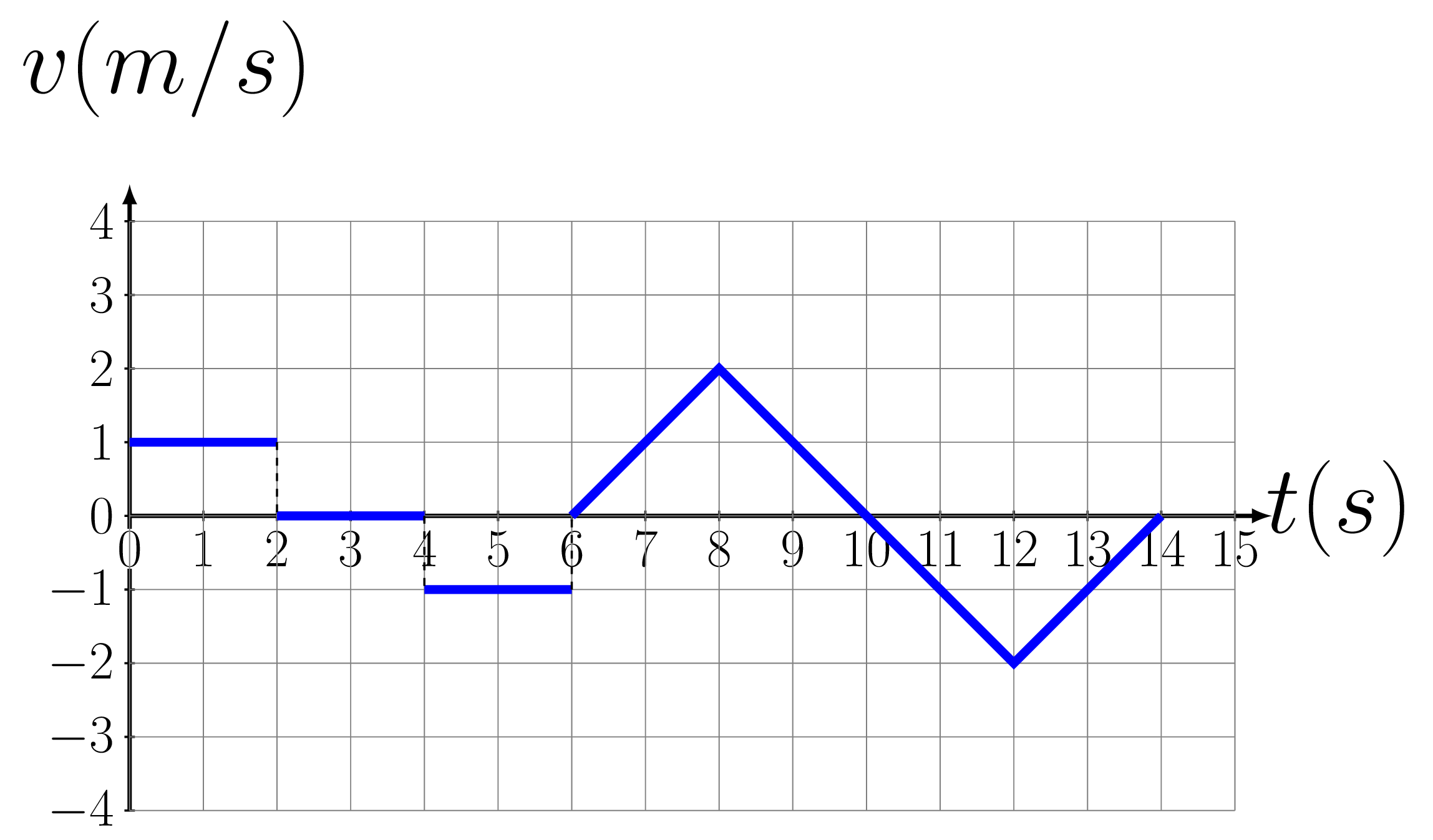
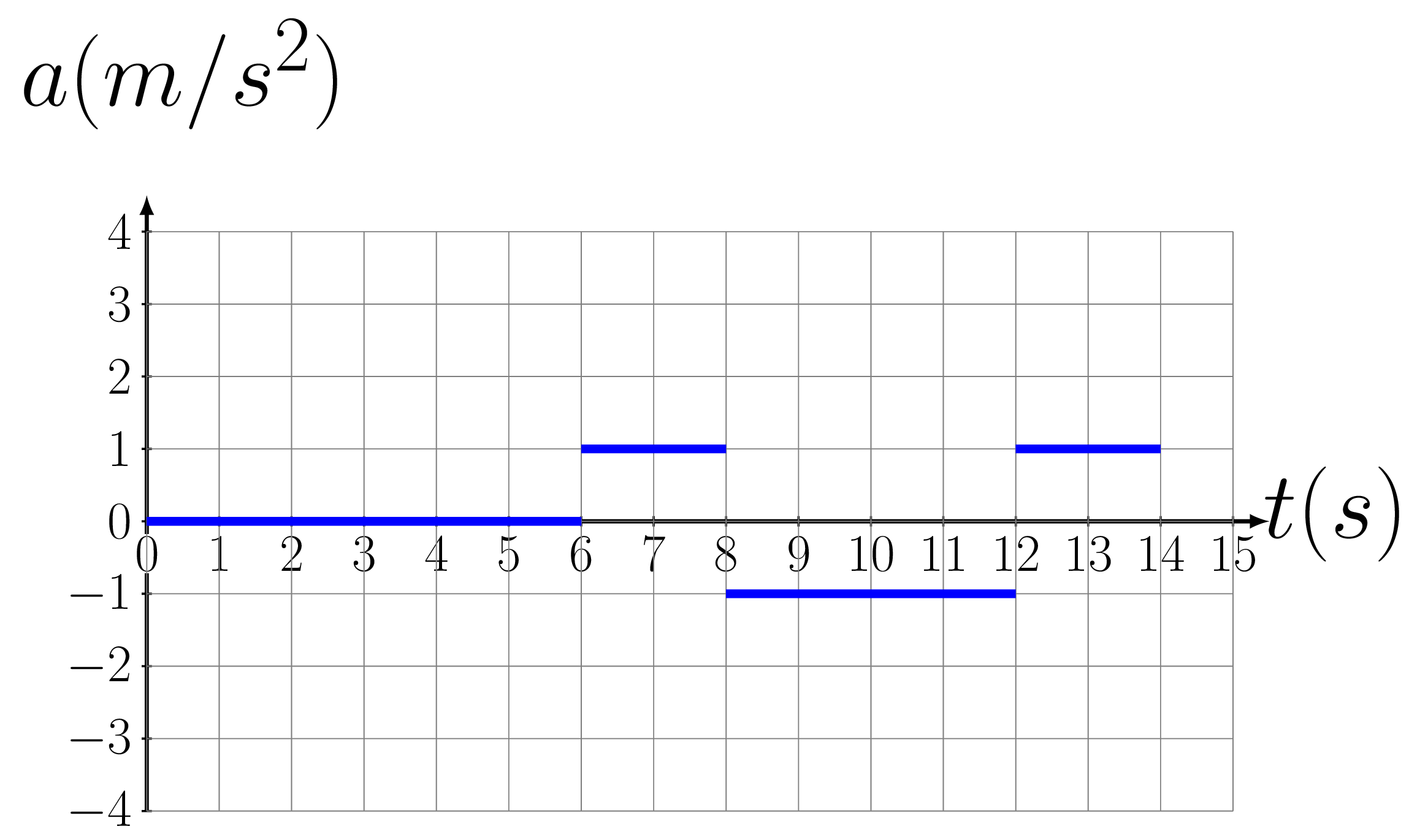
The specific features of motions can be read as follows from the graph: If position, x is increasing, then velocity, v is \(+ve\text{,}\) if position, x is decreasing, then velocity, v is \(-ve\text{,}\) if velocity, v is increasing, then acceleration, a is \(+ve\text{,}\) if velocity, v is decreasing, then acceleration, a is \(-ve\text{.}\) The slope of x \(x \sim t \) t graph gives velocity and the slope of \(v \sim t\) graph gives acceleration. The area under \(v \sim t\) graph gives position [\(x=vt\)] and the area under \(a \sim t\) graph gives velocity [\(v=at\)]. Note that even if the shape of these graphs look weird all the motions happen only in one dimension, i.e., going up or down with time Figure 3.1.7–3.1.8.(a).
From Figure 3.1.8.(a), slope of line AB=+ve, slope of line BC=0, and slope of line CD =-ve, which means the object is running with constant velocity along +ve direction, stays at rest, and again starts moving with constant velocity along -ve direction, respectively. The slope of bottom portion of curve DE =0 nd that at top portion is +ve hence the object is speeding up in +ve direction. The slope of bottom portion of curve EF =+ve and that at top portion =0, hence the object is slowing down in +ve direction. The slope of top portion of curve FG =0 and that at bottom portion is -ve, hence the object is speeding up in -ve direction. The slope of top portion of curve GH =-ve and that at bottom portion =0, hence the object is slowing down in -ve direction as can be verified in figure Figure 3.1.8.(b). If velocity is constant there is no acceleration and if velocity is increasing in +ve direction, acceleration is +ve, if velocity is decreasing in +ve direction, acceleration is -ve, if velocity is increasing in -ve direction, acceleration is -ve, if velocity is decreasing in -ve direction, acceleration is +ve as can be seen from graph Figure 3.1.8.(c).
