Subsection 7.1.1 Parallel axis theorem
The moment of inertia of a body depends upon the axis of rotation and there are many axes possible about which a body can rotate. Hence the parallel axis theorem provides a relationship between the moment of inertia of a body about an axis passing through its center of mass to any other axis of a body which is parallel to the axis through center of mass.
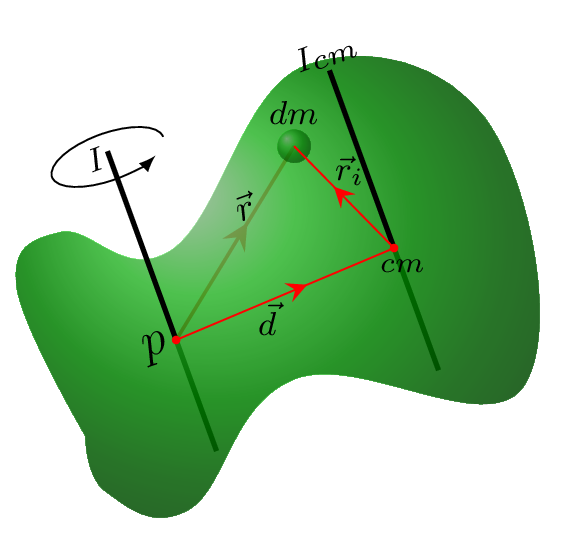
Consider an elementary mass \(m_{i}\) at a distance \(r_{i}\) from the center of mass of a body and at a distance \(r\) from the axis of rotation through a point p [Figure 7.1.2], then the moment of inertia of that point mass is given by
\begin{equation*}
I=\sum_{i} m_{i}r^{2} = \sum_{i} m_{i}\left(d+r_{i}\right)^{2}
\end{equation*}
\begin{equation*}
=\sum_{i} m_{i}\left(\vec{d}+\vec{r}_{i}\right)\cdot \left(\vec{d}+\vec{r}_{i}\right)
\end{equation*}
\begin{equation*}
=\sum_{i} m_{i}r^{2}_{i}+d^{2}\sum_{i} m_{i}+2\vec{d}\cdot\sum_{i} m_{i}r_{i}
\end{equation*}
In this expression \(\sum_{i} m_{i}r^{2}_{i}=I_{cm},\) a moment of inertia of the body about an axis through center of mass, \(\sum_{i} m_{i} =M\text{,}\) the mass of a body, \(I\text{,}\) moment of inertia of a body about an axis parallel to the axis through the center of mass, \(d,\) a distance between parallel axes, and
\begin{equation*}
\sum_{i} m_{i}r_{i}=\left(\frac{\sum_{i} m_{i}r_{i}}{M} \right)M \rightarrow 0.
\end{equation*}
Since the position of the center of mass lies at origin (0,0), i.e., \(r_{i}=0. \)
\begin{equation*}
\therefore \quad I = I_{cm} + M d^{2}
\end{equation*}
The parallel axis theorem states that the moment of inertia of a body about an axis parallel to an axis passing through the center of mass is equal to the sum of the moment of inertia of body about an axis passing through center of mass and product of mass and square of the distance between the two axes.
