Subsection 7.5.2 Simple Pendulum
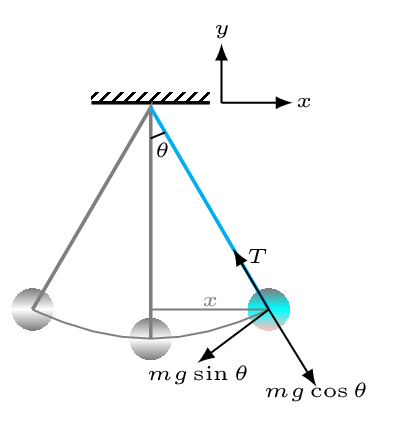
A simple pendulum consists of a heavy bob of mass \(m\) hanging from an inextensible and massless string of length \(l.\) When the bob is displaced from its mean position and released, it will swing back and forth with periodic motion as shown in Figure 7.5.6. From free body diagram, it is clear that \(mg\cos\theta \) is balanced by tension \(T\) in the string but unbalanced force \(mg\sin\theta \) provides the restoring force. Hence
\begin{equation*}
F_{s} = -mg\sin\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad ma = -mg\frac{x}{l}
\end{equation*}
\begin{equation*}
\text{or,}\quad a = -\frac{g}{l}x =-\omega^{2}x
\end{equation*}
where \(\omega = \sqrt{\frac{g}{l}} \) is the angular velocity of the bob performing circular motion. The time period of simple pendulum can be given as
\begin{equation*}
\omega = \frac{2\pi}{T}=\sqrt{\frac{g}{l}}
\end{equation*}
\begin{equation*}
\therefore \quad T = 2\pi\sqrt{\frac{l}{g}}
\end{equation*}
Alternative: The restoring torque Subsection 7.3.1 acting on the bob is given by
\begin{equation*}
\tau=-mgl\sin\theta
\end{equation*}
\begin{equation*}
or, \, I \alpha =ml^{2}\frac{\,d\omega}{\,dt}= ml^{2}\ddot{\theta}
\end{equation*}
As a restoring torque is giving a clockwise rotation when angular displacement is counterclockwise.
\begin{equation*}
\text{or,}\quad ml^{2}\ddot{\theta} =-mgl\sin\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad l\ddot{\theta} =-g\sin\theta =-g\theta \qquad [\text{small angle approximation}]
\end{equation*}
\begin{equation*}
\text{or,}\quad \ddot{\theta}+\frac{g}{l}\theta= 0
\end{equation*}
\begin{equation*}
\text{or,}\quad \ddot{\theta}+\omega^{2}\theta = 0 \qquad \left[\omega = \sqrt{\frac{g}{l}}\right]
\end{equation*}
This is second order differential equation the solution of which can be written as
\begin{equation*}
\theta(t) = \Theta(\sin\omega t + \phi)
\end{equation*}
where \(\Theta\) is called an angular amplitude.
