Subsection 10.6.11 Entropy
A natural tendency of systems is to lose order. When sugar is dissolved in water it becomes more randomized and will not reconstitute itself in the crystalline form again, unless we apply heat energy from outside of the system to evaporate water. When a hot and a cold body are put in contact to each other, heat energy begins to flow from the hot body to the cold body until they reach at thermal equilibrium. Heat will never move back the other way. To move heat from a cold body to a hot body an external work must be done by an external source such as a heat pump. Entropy is a measure of that disorderness. It is a measure of the system’s thermal energy per unit temperature that is unavailable for useful work. The concept of entropy provides the direction of spontaneous change for many process. It tells us that which process is allowed and which is completely prohibited even if it can not violet the fundamental law of conservation of energy. An ice cube placed on a hot pan surely melts, while the pan goes cooler. Such a process is called irreversible because no slight change will cause the melted water to turn back into ice while the pan goes hotter. In contrast, a block of ice placed in an ice water bath will either thaw a little more or freeze a little more, depending on whether a small amount of heat is added to or taken out from the system. Such a process is reversible because only an infinitesimal amount of heat is needed to change its direction from progressive freezing to progressive thawing.
Spontaneous change for an irreversible process in an isolated system always proceeds in a direction of increasing entropy. Entropy describes the degradation of energy to perform work. Crystals are more orderly than salt molecules in solution; however, vaporized water is more disordered than liquid water. The process taken as a whole results in a net increase in disorder. The first law of thermodynamics is the conservation of energy and is easy to express quantitatively. The second law explains that heat only flows from a hotter object to a colder one. It measures quantitatively that the efficiency of any reversible engine has to equal that of the Carnot cycle, and any irreversible engine has less efficiency. In the view of measuring the amount of irreversibility Clausius described a parameter, called entropy that doesn’t change in a reversible process but always increases in an irreversible one.
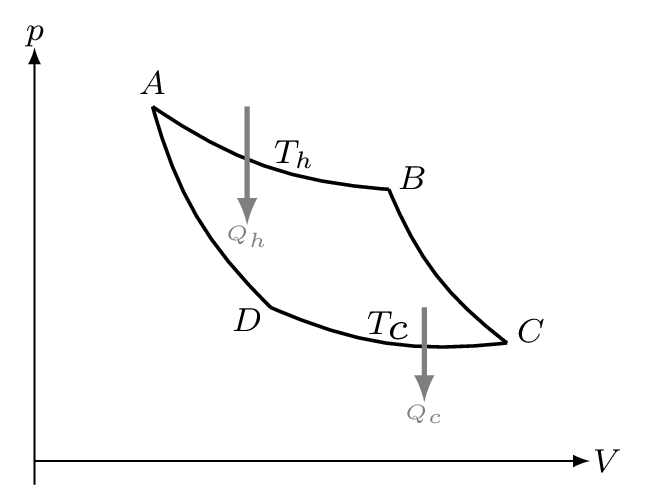
The total work done by the gas is the area of the curve ABCD. Hence the work done must be just the difference between the heat supplied at \(T_{h}\) and that dumped at \(T_{c}.\) Now the heat supplied along the initial hot isothermal path AB is equal to the work done along that curve,
\begin{equation*}
Q_{h}=nRT_{h}\ln\frac{V_{b}}{V_{a}}
\end{equation*}
and the heat dumped into the cold reservoir along CD is
\begin{equation*}
Q_{c}=nRT_{c}\ln\frac{V_{c}}{V_{d}}
\end{equation*}
The difference between these two is the net work output. This can be simplified using the adiabatic equations for the other two sides of the cycle:
\begin{equation*}
T_{h}V_{b}^{\gamma-1} = T_{c}V_{c}^{\gamma-1}
\end{equation*}
and
\begin{equation*}
T_{h}V_{a}^{\gamma-1} = T_{c}V_{d}^{\gamma-1}
\end{equation*}
On dividing of these two equations, we get -
\begin{equation*}
\frac{V_{b}}{V_{a}} =\frac{V_{c}}{V_{d}}
\end{equation*}
and using that in the preceding equation for \(Q_{c},\)
\begin{equation*}
Q_{c}=nRT_{c}\ln\frac{V_{b}}{V_{a}} = T_{c} \frac{Q_{h}}{T_{h}}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{Q_{c}}{Q_{h}}= \frac{T_{c}}{T_{h}}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{Q_{c}}{T_{c}}= \frac{Q_{h}}{T_{h}}
\end{equation*}
So for the Carnot cycle the ratio of heat supplied to heat dumped is just the ratio of the absolute temperatures. If we draw many isotherms and many adiabatics curve, then we can find in general that
\begin{equation*}
\frac{Q_{1}}{T_{1}}= \frac{Q_{2}}{T_{2}} = \frac{Q_{3}}{T_{3}} = \cdots = \frac{Q}{T} = constant
\end{equation*}
This quantity \(\frac{Q}{T}\) is a definite thermal property of the working substance. During adiabatic change, there is no transfer of heat so this quantity is zero. Hence that thermal property of the substance which remains constant during an adiabatic change is termed as entropy.
Now let see what happen if we take the path ADCBA. The amount of heat absorbed at temperature \(T_{h}\) when the gas passes from the state A to the state B remains constant even if a path other than the isotherm AB is followed. Now starting from the point A in reverse direction, let the path AD, DC, and CB be followed. Along the adiabatics AD and CB the quantity \(\frac{Q}{T} \) is zero and the quantity along the isothermal DC \(=\frac{Q_{c}}{T_{c}}.\) But we know that
\begin{equation*}
\frac{Q_{c}}{T_{c}}= \frac{Q_{h}}{T_{h}}
\end{equation*}
Hence the quantity \(\int\limits_{i}^{f} \frac{Q}{T}\) is independent of the manner of transformation, i.e., the entropy is a definite function of the thermal state of a body and is not affected in any way by the manner in which the particular state is reached. In other words, entropy is a definite physical entity like pressure, volume, temperature, or internal energy but there is nothing physical to represent it. Entropy can not be felt like pressure or temperature. Further, we can not measure the absolute entropy of a substance in any situation, we can only measure the change in entropy as the substance moves from one state to another. Entropy is denoted by a letter, \(S\text{.}\)
Change of entropy = heat energy/temperature
or, Change of entropy \(\times\) Temperature = Heat Energy.
That is the dimension of heat energy is same as that of the product of entropy and temperature. If we compare, gravitational potential energy \(\propto\) mass \(\times\) height with the above expression then it seems like, entropy bears to heat motion in the same fashion as mass bears to linear motion. Hence entropy is also known as a thermal inertia. The second law of thermodynamics can be stated in terms of entropy. The total entropy of the universe is continually increasing because all natural process is irreversible and entropy increases in irreversible process where as there is no change in entropy in the reversible process. But reversible process barely happen in the universe.
Differential form of change of entropy,
\begin{equation*}
\,dS = \frac{\,dQ}{T}
\end{equation*}
for reversible path.
Integral form
\begin{equation*}
\Delta S = S_{f} -S_{i}= \int\limits_{i}^{f} \frac{\,dQ}{T}
\end{equation*}
for reversible path.
Subsubsection 10.6.11.1 Principle of increase of entropy:
According to this principle, entropy of the universe always increases for any irreversible process, or remains constant for a reversible process.
- Change of entropy of the universe due to reversible process: Consider a Carnot cycle in isothermal expansion. The increase of entropy of the working substance is equal to \(\frac{Q_{h}}{T_{h}}.\) The decrease of entropy of the source is equal to \(\frac{Q_{h}}{T_{h}}. \) Thus the net change of entropy of universe during a reversible isothermal process is zero. There is no change of entropy during adiabatic process. Similarly, the decrease of entropy of the working substance during isothermal compression is \(\frac{Q_{c}}{T_{c}},\) the increases of entropy of the sink during isothermal compression is \(\frac{Q_{c}}{T_{c}}.\) Therefore, net change of entropy of the universe is zero. Now take the entire Carnot cycle at once, then loss of entropy of the source (surrounding) is \(\frac{Q_{h}}{T_{h}}\) and gains of entropy of the sink (surrounding) is \(\frac{Q_{c}}{T_{c}}\text{,}\) hence the net change of entropy of the universe,\begin{equation*} \,dS=\frac{Q_{c}}{T_{c}} -\frac{Q_{h}}{T_{h}}=0 \end{equation*}\begin{equation*} \therefore \quad \frac{Q_{c}}{T_{c}} =\frac{Q_{h}}{T_{h}} \end{equation*}The entropy of the whole system remains constant.
- Change of entropy of the universe due to irreversible process: Consider a heat transfer in conduction process. It is an irreversible process. Let a quantity \(\,dQ \) be transferred from a hot body A at a temperature \(T_{h}\) to a cold body B at temperature \(T_{c}.\) The loss of entropy of A is \(\frac{\,dQ}{T_{h}}\) and the gain of entropy of B is \(\frac{\,dQ}{T_{c}}.\) Thus the net change in entropy is\begin{equation*} \,dS= \frac{\,dQ}{T_{c}}-\frac{\,dQ}{T_{h}} = +ve \end{equation*}Since \(T_{h} \gt T_{c}\text{.}\) Therefore the entropy of the system as a whole increase during this process. The entropy of the universe increases in the irreversible process.
Subsubsection 10.6.11.2 Principle of degradation of entropy:
It states that the available energy of the universe is tending towards zero. From the second law whenever an irreversible process takes place, a certain quantity of energy of the universe is converted from a form in which it is unavailable for work. In Carnot engine, \(Q_{h}\) is the heat that is taken from a source and \(Q_{c}\) is the amount of heat given to the sink. The difference of this heat \(Q_{h}-Q_{c}\) is converted into work and is called the available energy. Available energy is therefore,
\begin{equation*}
Q_{h}-Q_{c} = Q_{h}\left(1-\frac{Q_{c}}{Q_{h}}\right) = Q_{h}\left(1-\frac{T_{c}}{T_{h}}\right)
\end{equation*}
\(\left[\because \frac{Q_{c}}{Q_{h}}=\frac{T_{c}}{T_{h}} \right]\) Thus the lower the temperature \(T_{c}\) of the sink, the greater will be the available energy.
Now consider an irreversible process in which heat Q is transferred from hot body at temperature \(T_{h}\) to a cold body at temperature \(T_{c}.\) Suppose \(T_{o}\) is the lowest available temperature in the system, then available energy to start with is \(Q\left(1-\frac{T_{o}}{T_{h}}\right).\) After transfer it becomes \(Q\left(1-\frac{T_{o}}{T_{c}}\right).\) Hence the loss available energy in the process of transformation is
\begin{equation*}
Q\left(1-\frac{T_{o}}{T_{h}}\right)- Q\left(1-\frac{T_{o}}{T_{c}}\right)
\end{equation*}
\begin{equation*}
= Q\left[\frac{T_{o}}{T_{c}}-\frac{T_{o}}{T_{h}}\right] = T_{o}\left(\frac{Q}{T_{c}}-\frac{Q}{T_{h}} \right)=T_{o}\,dS.
\end{equation*}
Since \(\,dS\) is increasing in irreversible process available energy is decreasing. All natural process are irreversible the available energy of the universe is continually decreasing. When a state of maximum entropy of the universe is reached there would be no available energy to do any work, this condition is called the heat-death.
