Subsection 4.7.1 Horizontal Circle
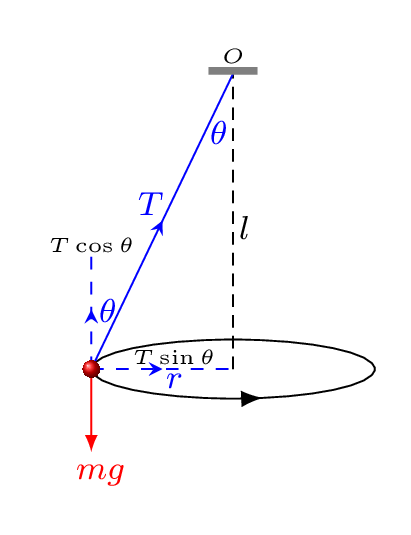
Horizontal Circle or a A conical pendulum is mass attached to a weightless and inextensible string over the rigid support and moves in a horizontal circle. Let us consider a body of mass, \(m\) tied with the string of length, \(l\) over the rigid support \(O\) and whirl in a horizontal circle of radius, \(r\text{.}\) At any instant of time the body is at \(P\) where the tension, \(T\) is acted along the string as shown in Figure 4.7.1. The vertical component of tension \(T\cos\theta\) balances \(mg\) and unbalanced the horizontal component \(T\sin\theta\) provides necessary centripetal force.
\begin{equation}
T\cos\theta=mg \tag{4.7.1}
\end{equation}
\begin{equation}
T\sin\theta=\frac{mv^{2}}{r} \tag{4.7.2}
\end{equation}
\begin{equation*}
\tan\theta=\frac{v^{2}}{rg}
\end{equation*}
\begin{equation*}
or, \quad \theta=\tan^{-1}\left(\frac{v^{2}}{rg}\right)
\end{equation*}
The time period \(T'\) can be given by
\begin{equation*}
T'=\frac{2\pi r}{v}= 2\pi\frac{r}{\sqrt{rg\tan\theta}}=2\pi\sqrt{\frac{r}{g\tan\theta}}
\end{equation*}
\begin{equation*}
= 2\pi\sqrt{\frac{l\sin\theta}{g\tan\theta}}=2\pi\sqrt{\frac{l\cos\theta}{g}}
\end{equation*}
If \(\theta \to 90^{o}\text{,}\) then tension in the string \(T \to \infty\text{,}\) which is not possible. Hence the body never receives the same height as its fixed support.
