Subsection 7.1.3 Moment of Inertia of a Ring or Hoop
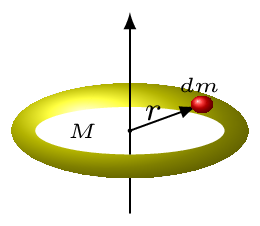
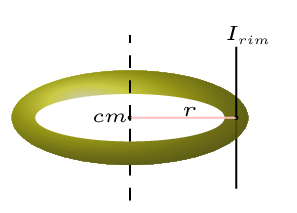
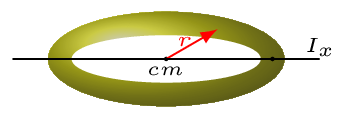
As moment inertia depends upon the shape, mass distribution, and position of axis of rotation. Here are some conditions discussed below for a ring.
Subsubsection 7.1.3.1 About an axis passing through its center of mass and perpendicular to its plane
Consider a small element of mass \(\,dm \) of a rim of the ring of radius \(r\) is rotating about an axis passing passing through its center of mass and perpendicular to its plane [Figure 7.1.4.(a)], then the moment of inertia of that elemental mass is given by
\begin{equation*}
\,dI=\,dm r^{2}.
\end{equation*}
Therefore moment of inertia of a whole ring about that axis is
\begin{equation*}
I=\int\,dI=\int\limits_{0}^{M}\,dm r^{2} = r^{2}\left.m\right|_{0}^{M}= Mr^{2} = I_{cm}
\end{equation*}
where \(M\) is the mass of the ring.
Subsubsection 7.1.3.2 About an axis passing through its rim and perpendicular to its plane
Consider a ring of mass \(M\) and radius \(r\) is rotating about an axis passing passing through its rim and perpendicular to its plane [Figure 7.1.4.(b)], then the moment of inertia of that ring can be obtained by
\begin{equation*}
I_{rim}=I_{cm}+Md^{2} = Mr^{2}+Mr^{2} =2Mr^{2}
\end{equation*}
Subsubsection 7.1.3.3 About an axis through its diameter
The moment of inertia of a ring about its center of mass and perpendicular to its plane [Figure 7.1.4.(c)], is
\begin{equation*}
I_{cm}=Mr^{2}.
\end{equation*}
Now using the perpendicular axis theorem, we have
\begin{equation*}
I_{z}=I_{x}+I_{y} =2I_{x}.
\end{equation*}
As ring is a symmetrical object \(I_{x}\) is considered as equal to \(I_{y}\text{.}\) Hence
\begin{equation*}
I_{cm}=I_{z}=Mr^{2}=2I_{x}
\end{equation*}
\begin{equation*}
\therefore\quad I_{x}= I_{y}=I_{diameter}=\frac{1}{2}Mr^{2}
\end{equation*}
