Examples

Section 6.3 Examples

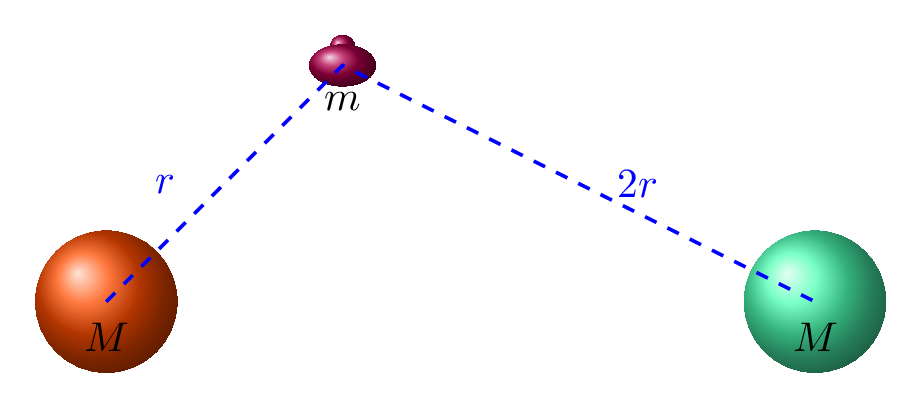
Example 6.3.1.

Consider the mass distribution shown at right. What is the magnitude and direction of initial acceleration of the 4 kg mass if all of the masses are released from rest out in space?

Solution.

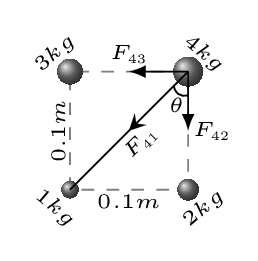
Given: \(m_{1} = 1 kg, \quad m_{2} = 2 kg, \quad m_{3} = 3 kg,\quad m_{4} = 4 kg, \) \(r_{21} = 0.1 m, \quad r_{31} = 0.1 m, \quad G = 6.67 \times 10^{-11} Nm^{2}/kg^{2}.\)

Equations:

\begin{equation*} \tan\theta = \frac{0.1}{0.1} \Rightarrow \theta =\tan^{-1}1 =45^{o}, \end{equation*}

\begin{equation*} r_{41}=\sqrt{0.1^{2}+0.1^{2}}=0.1414m, \end{equation*}

\begin{equation*} F_{41} = G \frac{m_{1}m_{4}}{r_{41}^{2}} = G\frac{1 \times 4}{0.02}=(200G) N, \end{equation*}

\begin{equation*} F_{42} = G \frac{m_{4}m_{2}}{r_{42}^{2}} = G \frac{2\times4}{0.01}= (800G) N, \end{equation*}

\begin{equation*} F_{43} = G\frac{4 \times 3}{0.01}=(1200G) N, \end{equation*}

\begin{equation*} \sum F_{x} = F_{43} + F_{41} \sin\theta = -8.9\times10^{-8} N; \end{equation*}

\begin{equation*} \quad \sum F_{y} = F_{42} + F_{41} \cos\theta = -6.2\times10^{-8} N \end{equation*}

\begin{equation*} \therefore F=\sqrt{F^{2}_{x} +F^{2}_{y}} = 1.08\times10^{-7}N; \quad \phi=\tan^{-1}\left(\frac{F_{y}}{F_{x}}\right) = 35^{o} \end{equation*}

The direction of resultant force is acting along \(35^{o}\) below the x-axis, which is also the direction of resultant acceleration of mass 4 kg.

\begin{equation*} F=m_{4}a \qquad \Rightarrow \quad a=\frac{F}{m_{4}} =\frac{1.08\times10^{-7}N}{4kg} =2.7\times10^{-8}m/s^{2} \end{equation*}

Example 6.3.2.

A satellite orbits the earth in a circular orbit at an altitude of 1000 mile.

What is its orbital speed?
How long does it take to complete one orbit?

Solution.

Given: \(G = 6.67\times 10^{-11} N.m^{2}/kg^{2},\) \(h = (1000 mile) \times (1.609 \frac{km}{mile})\times(1000 \frac{m}{km}) = 1.609\times 10^{6}m, \) \(R = 6.37\times 10^{6} m, \quad M = 5.98\times 10^{24} kg.\)

Equations:

\begin{equation*} r = R + h = 7.979\times 10^{6} m, \quad v_{o} =\sqrt{\frac{GM}{r}} = 7.07km/s \end{equation*}

\begin{equation*} T=\frac{2\pi r}{v_{o}} = \frac{2\times\pi\times(7.979\times 10^{6})}{7.07\times10^{3}}= 1.97 h \end{equation*}

Example 6.3.3.

A rocket is launched straight up from the surface of the planet of mass \(3\times10^23 kg\) and radius \(1.2\times10^{7} m\) at twice the escape speed. What is the speed of the rocket far away from the planet?

Solution.

Given:

\begin{equation*} v_{l}=2v_{e}, \quad M=3\times10^23 kg, \quad r =1.2\times10^{7} m, \quad v_{\infty}=? \end{equation*}

\begin{equation*} E_{planet}= E_{\infty} \end{equation*}

\begin{equation*} \text{or,}\quad \frac{1}{2}mv_{l}^{2}-\frac{GMm}{r}=\frac{1}{2}mv_{\infty}^{2} \end{equation*}

\begin{equation*} \text{or,}\quad\frac{1}{2}m(2v_{e})^{2}-\frac{GMm}{r}=\frac{1}{2}mv_{\infty}^{2} \end{equation*}

\begin{equation*} \text{or,}\quad 4\left(\frac{1}{2}m(v_{e})^{2}\right)-\frac{GMm}{r}=\frac{1}{2}mv_{\infty}^{2} \end{equation*}

\begin{equation*} \text{or,}\quad 4\left(\frac{GMm}{r}\right)-\frac{GMm}{r}=\frac{1}{2}mv_{\infty}^{2} \end{equation*}

\begin{equation*} \therefore \frac{3GM}{r}=\frac{1}{2}v_{\infty}^{2} \end{equation*}

\begin{equation*} v_{\infty}= \sqrt{\frac{6GM}{r}} = 3163m/s. \end{equation*}

Example 6.3.4.

A starship in a binary system is located a distance r from one star and a distance 2r from the other star. The starship wants to launch a deep space probe of mass m. The probe has no propulsion system of its own. What is the escape velocity from the starship’s current location in the binary star system above?

Solution.

From the energy conservation, total energy at starship = 0.

That is total potential energy at starship = kinetic energy for escaping the probe at starship.

\begin{equation*} E_{1}+E_{2}=E \end{equation*}

\begin{equation*} 0-\frac{GMm}{r}+0-\frac{GMm}{2r}+\frac{1}{2}mv_{e}^{2} =0 \end{equation*}

\begin{equation*} \therefore\quad v_{e} =\sqrt{\frac{3GM}{r}} \end{equation*}

Example 6.3.5.

Two satellites of equal masses m revolve around the planet of mass M. The planet’s mass is much larger than the mass of the satellites, \(m \lt \lt M\text{.}\) The radii of the orbits of the satellites are r and 2r. The satellites are connected by a light string, directed along the radius of the orbit, that keeps their periods of revolution equal. Find the force of tension T in the string in terms of m, M, r, and G. What is the period \(\tau\) of the satellites’ orbit? Answer in terms of G, r, and M, and mathematical constants.

Solution.

Let \(\omega\) be the angular velocity of satelites, then centripetal force needed for first satelite is given by

\begin{equation} \frac{GMm}{r^{2}}-T_{12} = mr\omega^{2} \tag{6.3.1} \end{equation}

centripetal force needed for second satelite is given by

\begin{equation*} \frac{GMm}{(2r)^{2}}+T_{21} = m(2r)\omega^{2} \end{equation*}

\begin{equation} \therefore \frac{GMm}{4r^{2}}+T_{21} = 2mr\omega^{2}\tag{6.3.2} \end{equation}

From eqns. (6.3.1) and (6.3.2), we get -

\begin{equation*} \frac{GMm}{4r^{2}}+T_{21} = 2\left[\frac{GMm}{r^{2}}-T_{12}\right] = \frac{2GMm}{r^{2}}-2T_{12} \end{equation*}

\begin{equation*} \text{or,}\quad \frac{GMm}{4r^{2}}- \frac{2GMm}{r^{2}} = 2T_{12} - T_{21} = -3T \end{equation*}

\([\because T_{21}=T_{12}=T]\)

\begin{equation*} \therefore \quad T = \frac{7}{12}\left(\frac{GMm}{r^{2}}\right) \end{equation*}

Now, from eqn (6.3.1),

\begin{equation*} [v_{1} = \frac{5GM}{12r} \end{equation*}

and hence,

\begin{equation*} \tau = \frac{2\pi r}{v_{1}} = \sqrt{\frac{48\pi^{2}r^{3}}{5GM}} \end{equation*}

\([\because v=r\omega]\)

Example 6.3.6.

Two asteroids of masses M and m and radii R and r are at rest and isolated in space at a distance d apart. They begin drifting towards each other and smashed eventually. If M = 4m and R = 2r, find the velocity of the small asteroid just before it hits the big asteroid.

Solution.

From conservation of momentum

\begin{equation*} M u_{1} - m u_{2} = 0 \end{equation*}

\begin{equation*} \text{or,}\quad 4mu_{1} = mu_{2} \end{equation*}

\begin{equation*} \therefore\quad u_{1} =\frac{u_{2}}{4} \end{equation*}

Also from conservation on energy,

\begin{equation*} -\frac{GMm}{d} =-\frac{GMm}{R+r}+\frac{1}{2}Mu_{1}^{2} +\frac{1}{2}mu_{2}^{2} \end{equation*}

\begin{equation*} \text{or,}\quad -\frac{G4mm}{d} =-\frac{G4mm}{3r}+\frac{1}{2}4mu_{1}^{2} +\frac{1}{2}mu_{2}^{2} \end{equation*}

\begin{equation*} \text{or,}\quad -\frac{G4m}{d} +\frac{G4m}{3r}= 2\left(\frac{u_{2}}{4}\right)^{2} +\frac{1}{2}u_{2}^{2} \end{equation*}

\begin{equation*} \text{or,}\quad 4Gm\left[\frac{1}{3r}-\frac{1}{d} \right] \end{equation*}

\begin{equation*} = \left(\frac{1}{8}+\frac{1}{2}\right) u_{2}^{2} = \frac{5}{8} u_{2}^{2} \end{equation*}

\begin{equation*} \therefore\quad u_{2} = \sqrt{\frac{32}{5}Gm\left(\frac{1}{3r}-\frac{1}{d}\right)} \end{equation*}

Prev Top Next