Subsection 5.1.6 Loop-the-Loop Track
A loop-the-loop track consists of an incline plane that leads into a circular loop of radius \(r\text{.}\) When a body at rest is released from a certain minimum height \(h_{min}\) of the inclined plane it will make around the loop without falling. Assuming no friction during motion. The height of the ramp from where the body is released must be so chosen that when the body reaches at the top of the loop, it must be moving with the certain minimum velocity in order to have necessary centripetal force. At the top point B of the loop the weight \(w\) and normal force \(N\) are acting on the body downward. These forces must be providing a necessary centripetal force. Remember centripetal force is a resulting force it is not something that acts on the body. It must be provided by some other causing forces which can act on the body. Hence at point B,
\begin{equation*}
N+w=F_{c}
\end{equation*}
\begin{equation*}
\text{or,}\quad N+mg=\frac{mv_{B}^{2}}{r}
\end{equation*}
For \(v_{B}\) to be minimum, \(N\to 0\text{.}\)
\begin{equation*}
\therefore mg = \frac{mv_{min}^{2}}{r}
\end{equation*}
\begin{equation*}
g=\frac{v_{min}^{2}}{r}
\end{equation*}
\begin{equation}
\therefore v_{min} = \sqrt{gr} \tag{5.1.4}
\end{equation}
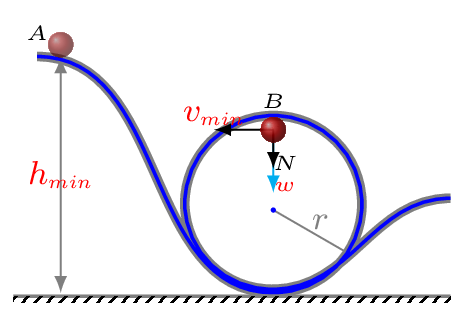
Now from the principle of conservation of energy
\begin{equation*}
E_{B} = E_{A}.
\end{equation*}
\begin{equation*}
\text{or,}\quad KE_{B}+PE_{B}=KE_{A}+PE_{A}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{1}{2}mv_{B}^{2}+mg(2r)=0+mgh_{A}
\end{equation*}
For \(h_{A}\) to be \(h_{min}\text{,}\) \(v_{B} = v_{min}.\)
\begin{equation*}
\text{or,}\quad \frac{1}{2}mv_{min}^{2}+mg(2r)=mgh_{min}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{1}{2}m(gr)+mg(2r)=mgh_{min}
\end{equation*}
[from eqn. (5.1.4)]
\begin{equation}
\therefore h_{min} = \frac{r}{2}+2r =\frac{5}{2} r\tag{5.1.5}
\end{equation}
If the height of incline (ramp) is less than \(\frac{5r}{2} \) the body will not make a complete cycle around the loop and must fall during its vertical motion inside the loop.
