Subsection 3.3.1 Projtile Motion
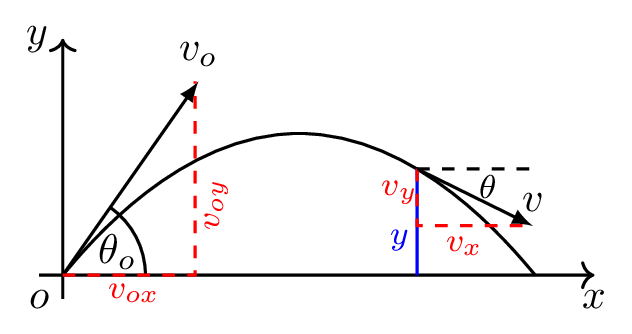
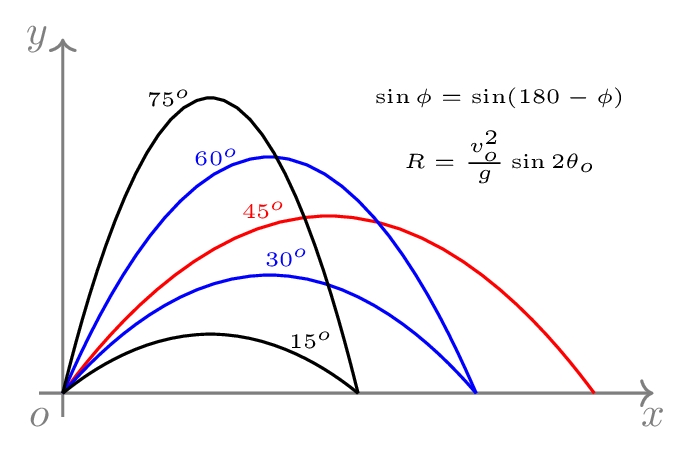
Projectile is a particle which has both horizontal as well as vertical motions. For example, a baseball in flight is a projectile. To analyze the projectile motion, three basic assumptions are made:
- acceleration due to gravity is constant and is directed downward,
- the effect of air resistance is negligible, and
- the surface of the earth is flat.
To analyze the projectile motion, two‐dimensional motion is separated into vertical and horizontal motions. The object in vertical motion experiences constant acceleration due to gravity. The object in horizontal motion on the other hand experiences no acceleration and hence it maintains a constant horizontal velocity through out its motion. Suppose a particle is thrown from the origin with an initial velocity (\(v_{o}\)), along an angle \(\theta_{o}\) from the ground level as shown in Figure 3.3.1.(a), then the x- and y- components of the initial velocity are given by
\begin{equation}
v_{ox} = v_{o}\cos\theta_{o} \tag{3.3.1}
\end{equation}
and
\begin{equation}
v_{oy} = v_{o}\sin\theta_{o} \tag{3.3.2}
\end{equation}
The horizontal distance covered by the projectile in any time \(t\) is given by
\begin{equation}
x = v_{ox} t \qquad [\because a=constant]\tag{3.3.3}
\end{equation}
The vertical distance covered by the projectile in any time \(t\) is given by
\begin{equation}
y = v_{oy} t - \frac{1}{2} g t^{2} \qquad [\because a=-g] \tag{3.3.4}
\end{equation}
here \(g\) is taken as positive for downward direction. Hence velocities and angle of a projectile after time \(t\) is given by
\begin{equation}
v_{x} = v_{ox} \tag{3.3.5}
\end{equation}
\begin{equation}
v_{y} = v_{oy} - g t \tag{3.3.6}
\end{equation}
and
\begin{equation}
\tan\theta = \frac{v_{y}}{v_{x}} \quad \Rightarrow \theta =tan^{-1}\left( \frac{v_{y}}{v_{x}}\right) \tag{3.3.7}
\end{equation}
The time taken by the projectile to reach its highest point, \(H\) and falls to the ground again is called a time of flight \(T\text{.}\) The time for the projectile to reach the ground from its highest point is equal to the time of fall for a freely falling object that falls straight down from the same height. This is because an object in flight only experiences vertical force (weight of the object) in vertical motion but not in horizontal motion as soon as it is released from the thrower’s hand. Projectile paths are parabolic and, therefore, symmetric. The object reaches the top of its rise in half of the total time of flight \(T\text{.}\) At the top of the rise, the vertical velocity is zero. These facts can be used to derive the horizontal distance traveled by the projectile, also called the range \(R\text{.}\) At maximum height, \(v_{y} = 0\) and \(t = \frac{T}{2}\text{;}\) therefore, the time of flight using eqns. (3.3.6) and (3.3.2)
\begin{equation*}
0= v_{oy} - g t = v_{o}\sin\theta_{o} -g\frac{T}{2}
\end{equation*}
\begin{equation}
\therefore \quad T = \frac{2v_{o}\sin\theta_{o}}{g}\tag{3.3.8}
\end{equation}
\begin{equation*}
x=v_{ox}t
\end{equation*}
or,
\begin{equation*}
R=v_{o}\cos\theta_{o}T = v_{o}\cos\theta_{o}\left(\frac{2v_{o}\sin\theta_{o}}{g}\right)
\end{equation*}
\begin{equation}
\therefore R = \frac{v_{o}^{2}\sin 2\theta_{o}}{g} \qquad [\because 2\sin\theta\cos\theta =\sin 2\theta]\tag{3.3.9}
\end{equation}
The maximum height \(H\) is given by
\begin{equation*}
v^{2}_{f} = v^{2}_{o}+2as
\end{equation*}
\begin{equation*}
\text{or,} \quad 0=v^{2}_{oy}-2gH
\end{equation*}
\begin{equation}
\therefore H= \frac{v^{2}_{oy}}{2g} = \frac{v^{2}_{o}\sin^{2}\theta_{o}}{2g}\tag{3.3.10}
\end{equation}
If \(\theta_{o} = 45^{o}\text{,}\) then \(R = \frac{v_{o}^{2}\sin 90}{g} = \frac{v_{o}^{2}}{g}\) is maximum using eqn. (3.3.9). Figure 3.3.1.(b) sketches the trajectories of projectiles thrown with the same initial speed at different angles of inclination. The trajectory of a projectile is parabolic in nature as can be seen from eqns.(3.3.4) and (3.3.3),
\begin{equation*}
y=v_{oy}t-\frac{1}{2}gt^{2} = v_{oy}\left(\frac{x}{v_{ox}}\right)-\frac{g}{2}\left(\frac{x}{v_{ox}}\right)^{2}
\end{equation*}
\begin{equation*}
=\left(\frac{v_{o}\sin\theta_{o}}{v_{o}\cos\theta_{o}}\right)x - \frac{g}{2}\left(\frac{x}{v_{o}\cos\theta_{o}}\right)^{2}
\end{equation*}
\begin{equation}
\therefore y=\tan\theta_{o}x-\left(\frac{g}{2v_{o}^{2}\cos^{2}\theta_{o}}\right)x^{2} \tag{3.3.11}
\end{equation}
which resembles the parabolic equation \(y=ax+bx^{2}\text{.}\)
