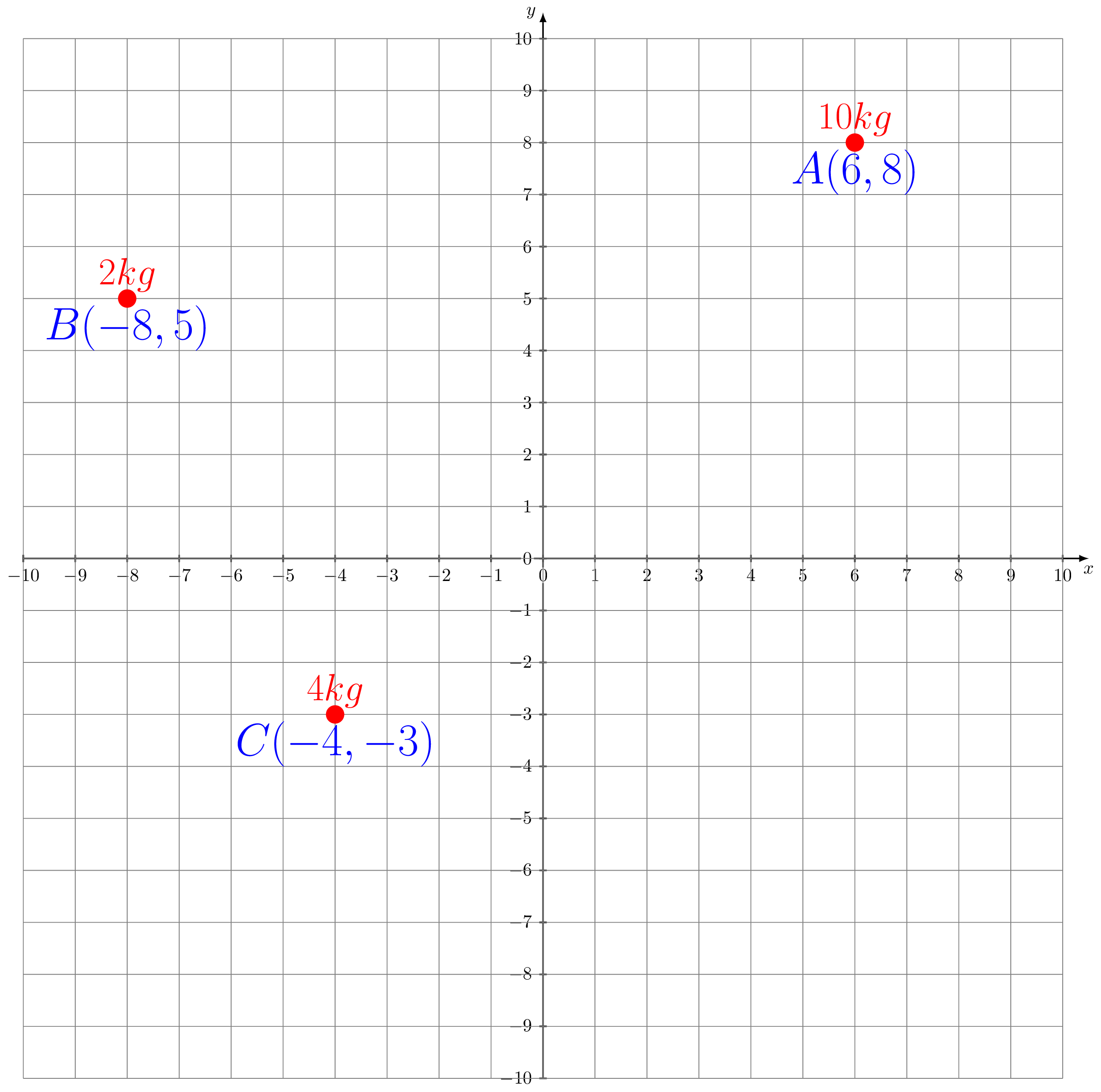
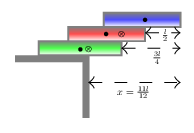
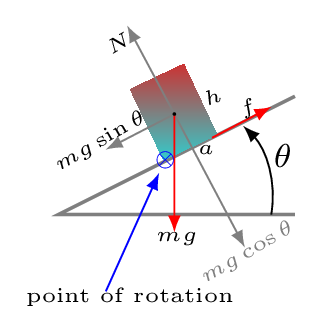
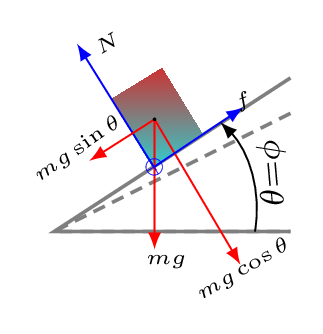
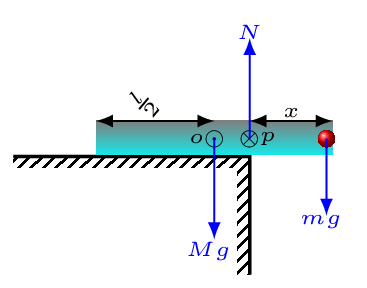
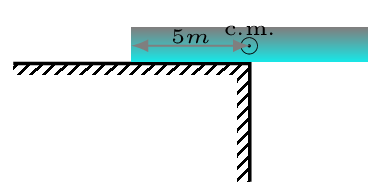Block(s) can be balanced at the edge of anything if its center of mass lies before edge or at least at the edge of that thing.
Maximum overhung = center of mass of blocks system.
Maximum overhung for blue (I) brick = its center of mass from the free end =\(\frac{l}{2} \text{.}\)
Center of mass for red (II) and blue (I) bricks
\begin{equation*}
= \left\{\frac{m\frac{l}{2}+m\left(\frac{l}{2}+\frac{l}{2}\right)}{2m}\right\} =\frac{3l}{4}.
\end{equation*}
Center of mass for green (III), red (II) and blue (I) bricks
\begin{equation*}
= \left\{\frac{2m\frac{3l}{4}+m\left(\frac{3l}{4}+\frac{l}{2}\right)}{3m}\right\} =\frac{11l}{12}.
\end{equation*}
Which is the maximum overhung for three bricks system. Using torque equation
Section 4.11, we can get same condition, if we set
\(x_{n}(nM) = x_{1}M\text{.}\) Where
\(x_{1}\) is C.M. of first object, and
\(n\) stands for number of objects. Maximum overhung,
\begin{equation*}
x= x_{1}+x_{2}+x_{3}+\cdots.
\end{equation*}
For example, in three books system like above: we have for first book
\begin{equation*}
x_{1} =\frac{l}{2}
\end{equation*}
for second book
\begin{equation*}
x_{2}(2M) =\frac{l}{2}M
\end{equation*}
\begin{equation*}
\therefore x_{2} =\frac{l}{4}
\end{equation*}
for third book
\begin{equation*}
x_{3}(3M) =\frac{l}{2}M
\end{equation*}
\begin{equation*}
\therefore x_{3} =\frac{l}{6}
\end{equation*}
Hence, maximum overhung,
\begin{equation*}
x=\frac{l}{2} + \frac{l}{4} +\frac{l}{6} = \frac{11l}{12}
\end{equation*}
The general rule to find the maximum overhung,x for a uniform object is
\begin{equation*}
x= l\sum_{n=1}^{n}\left(\frac{1}{2n}\right)
\end{equation*}