Subsection 7.1.6 Moment of Inertia of a Plate
Subsubsection 7.1.6.1 About an axis \(I_{x}\) passing through its center of mass and parallel to its plane
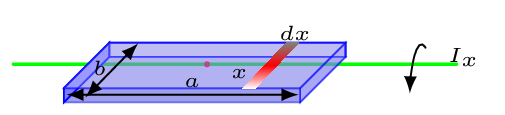
Consider a plate of length \(a\) and width \(b\) is made out off number of elementary rods of thickness \(\,dx\text{,}\) then moment of inertia of that rod about x-axis is given by
\begin{equation*}
I_{x} = \int x^{2}\,dm = \int\limits_{0}^{a}\frac{1}{12}\,dmb^{2}
\end{equation*}
here \(\,dm\) = (mass per unit area)(area of a rod), by considering neglible plate thickness.
\begin{equation*}
\therefore \quad I_{x} = \frac{1}{12}b^{2}\int\limits_{0}^{a}\frac{M}{ab}b\,dx
\end{equation*}
\begin{equation*}
= \frac{Mb^{2}}{12a}\left.x\right|_{0}^{a} = \frac{1}{12}Mb^{2}
\end{equation*}
Subsubsection 7.1.6.2 About an axis \(I_{y} \) passing through its center of mass and parallel to its plane
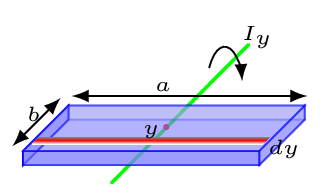
Consider a plate of length \(a\) and width \(b\) is made out off number of elementary rods of thickness \(\,dy\text{,}\) then moment of inertia of that rod about y-axis is given by
\begin{equation*}
I_{y} = \int y^{2}\,dm = \int\limits_{0}^{b}\frac{1}{12}\,dma^{2}
\end{equation*}
\(\,dm\) = (mass per unit area)(area of a rod), by considering neglible plate thickness.
\begin{equation*}
\therefore \quad I_{y} = \frac{1}{12}a^{2}\int\limits_{0}^{b}\frac{M}{ab}a\,dy = \frac{1}{12}Ma^{2}
\end{equation*}
Subsubsection 7.1.6.3 About an axis passing through its center of mass and perpendicular to its plane
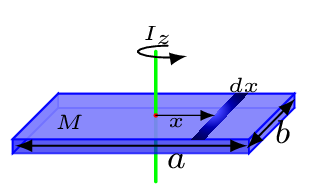
Consider a plate of length \(a\) and width \(b\) is made out off number of elementary rods of thickness \(\,dx\text{,}\) then moment of inertia of that rod about z-axis is given by
\begin{equation*}
\,dI_{z} = \left[\,dI_{cm}+\,dm \,x^{2}\right]\quad [\text{parallel axis theorem}]
\end{equation*}
\begin{equation*}
\text{or,}\quad \,dI_{z} = \left[\frac{1}{12}\,dm\,b^{2}+\,dm \,x^{2}\right]
\end{equation*}
\begin{equation*}
\text{or,}\quad \,dI_{z} = \left[\frac{1}{12}\left(\frac{M}{ab}b\,dx\right)\,b^{2}+\left(\frac{M}{ab}b\,dx\right) \,x^{2}\right]
\end{equation*}
\begin{equation*}
\,dm = \text{(mass per unit area)}(\text{area of a rod})
\end{equation*}
Hence the moment of inertia of a plate about center of mass is given by
\begin{equation*}
I_{z}=\int\,dI_{z} = \frac{M}{a}\int\limits_{-\frac{a}{2}}^{\frac{a}{2}}\left[\frac{1}{12}b^{2}\,dx +x^{2}\,dx \right]
\end{equation*}
\begin{equation*}
= \frac{M}{a}\left[\frac{1}{12}b^{2}\left.x\right\vert_{-\frac{a}{2}}^{\frac{a}{2}} +\left.\frac{x^{3}}{3}\right\vert_{-\frac{a}{2}}^{\frac{a}{2}} \right]
\end{equation*}
\begin{equation*}
I_{z} =\frac{M}{a}\left[\frac{1}{12}b^{2}\left(\frac{a}{2}+\frac{a}{2}\right)+\frac{1}{3}\left(\frac{a^{3}}{8}+ \frac{a^{3}}{8}\right)\right]
\end{equation*}
\begin{equation*}
=\frac{M}{12}\left[a^{2}+b^{2}\right]
\end{equation*}
Alternative: Moment of inertia of plate about \(I_{z}\) using perpendicular axis theorem,
\begin{equation*}
I_{z}=I_{x}+I_{y} = \frac{1}{12}Mb^{2}+\frac{1}{12}Ma^{2}
\end{equation*}
\begin{equation*}
=\frac{M}{12}\left(a^{2}+b^{2}\right)
\end{equation*}
