Subsection 8.1.1 Elastic Modulus
From Hook’s law,
\begin{equation*}
\sigma \propto \epsilon
\end{equation*}
\begin{equation*}
\text{or,}\quad \sigma = E. \epsilon
\end{equation*}
where \(E\) is a proportionality constant, called modulus of elasticity. It is a material property which defines how stiff is the material.
\begin{equation*}
\text{or,}\quad E= \frac{\sigma}{\epsilon}
\end{equation*}
Hence modulus of elasticity, \(E\) defines stress per unit strain. Its unit is Pascal (Pa). In the deformation process material stores energy in the form of potential energy or dissipates energy plastically. Stress is not directly measurable. We can calculate stress differently using applied tension, tangential force, compressional force, etc.
Subsubsection 8.1.1.1 Young’s Modulus or Elasticity of Length
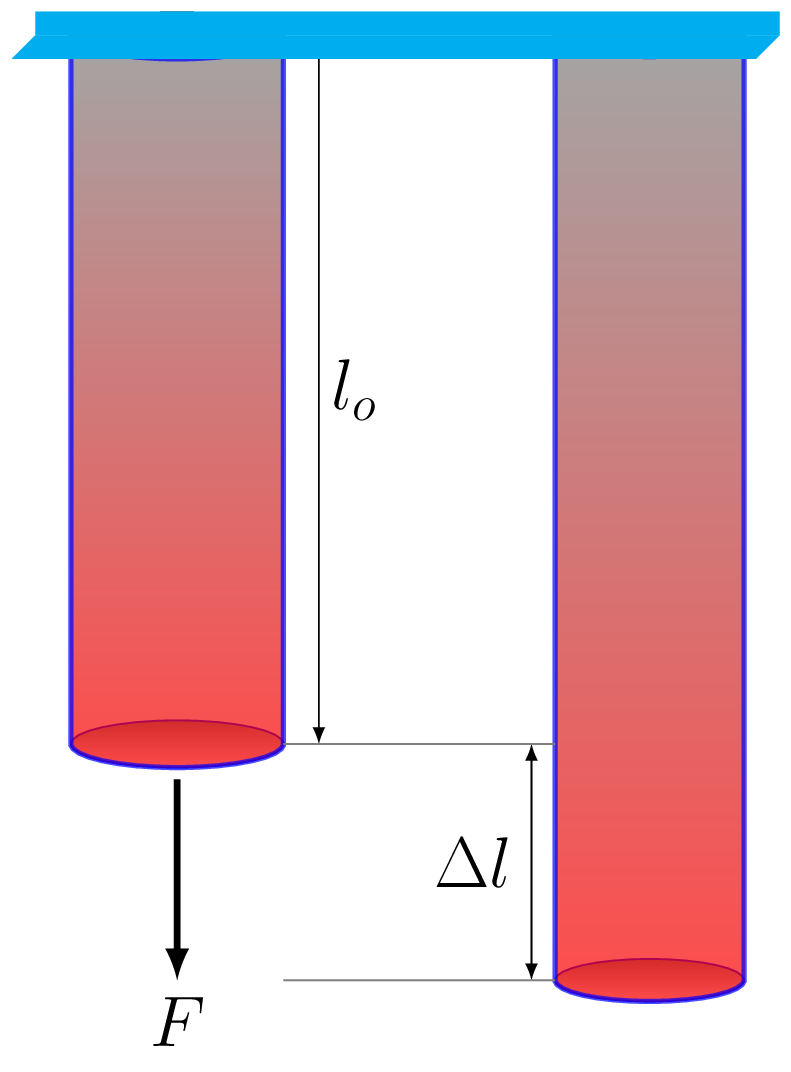
Consider a rod of length \(l_{o}\) whose top face is fixed and a normal force \(F\) is being applied on its bottom face as shown in Figure 8.1.2, then from Hook’s law, normal (tensile) stress \(\propto\) longitudinal strain, that is
\begin{equation*}
\frac{F}{A} =Y \frac{\Delta l}{l_{o}}
\end{equation*}
where \(Y\) is called Young’s modulus, \(A\) is cross-sectional area of wire, and \(l_{o}\) is an original length. Hence
\begin{equation*}
Y= \frac{Fl_{o}}{A\Delta l}
\end{equation*}
Its unit is \(N/m^{2} or, \,Pascal.\) When a wire under tension is elongated, its width is slightly diminished. This lateral shrinkage constitutes a transverse strain that is equal to the change in the width divided by the original width, i.e.,
\begin{equation*}
e_{trans} = \frac{\Delta D}{D}
\end{equation*}
The ratio of the lateral contraction (transverse strain) to the elongation (longitudinal strain) is called Poisson’s ratio.
\begin{equation*}
\therefore \quad \eta = -\frac{e_{trans}}{e_{long}} = -\frac{\Delta D/D}{\Delta l/l_{o}}
\end{equation*}
Tensile deformation is considered positive and compressive deformation is considered negative. The material which does not contract is brittle and the one which contracts is ductile. Poisson ratio of any material lies between 0 to 0.5.
Subsubsection 8.1.1.2 Bulk Modulus or Elasticity of Volume
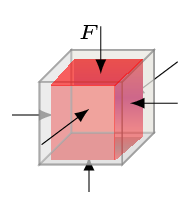
Consider a cube of surface area \(A\) whose volume is being compressed by applying a deforming force \(F\) as shown in Figure 8.1.3. Now from Hook’s law, volumetric stress \(\propto\) volumetric strain, that is
\begin{equation*}
\frac{F}{A} =B \frac{\Delta V}{V}
\end{equation*}
where \(B\) is called bulk modulus or coefficient of volumetric elasticity. Hence
\begin{equation*}
B = \frac{\frac{F}{A}}{\frac{\Delta V}{V}} =\frac{FV}{A\Delta V}
\end{equation*}
Here \(F\) is a deforming force, \(A\) is surface area of a cube, \(\Delta V\) is change in volume \(V\text{,}\) and \(-ve\) sign shows compression.
Subsubsection 8.1.1.3 Shear Modulus (Modulus of Rigidity) or Elasticity of Shape
When a tangential force is applied on one of the faces of any material keeping opposite face fixed, it deforms its shape. Hence from Hook’s law, shear stress \(\propto\) shear strain. The elastic property of a body that causes the shape of the body to be changed when a stress is applied is called shear stress. The angle of shear, which is a measure of how much the body’s shape has been deformed is called shear strain. When the shear stress is removed the body returns to its original shape.
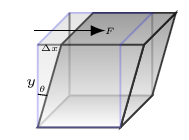
Consider a cube of sides y whose bottom face is fixed and a tangential force \(F\) is being applied on its top face as shown in Figure 8.1.4, then from Hook’s law, shear stress \(\propto \) shear strain, that is
\begin{equation*}
\frac{F}{A} =\sigma \frac{\Delta x}{y}
\end{equation*}
where \(\sigma \) is called modulus of shape or shear modulus. Hence
\begin{equation*}
\sigma = \frac{\frac{F}{A}}{\frac{\Delta x}{y}} =\frac{\frac{F}{A}}{\theta} =\frac{F}{A\theta}
\end{equation*}
Here \(F\) is a deforming force, \(A\) is surface area of a cube, and \(\theta \) is a shear angle.
