Subsection 5.1.5 Energy Diagram
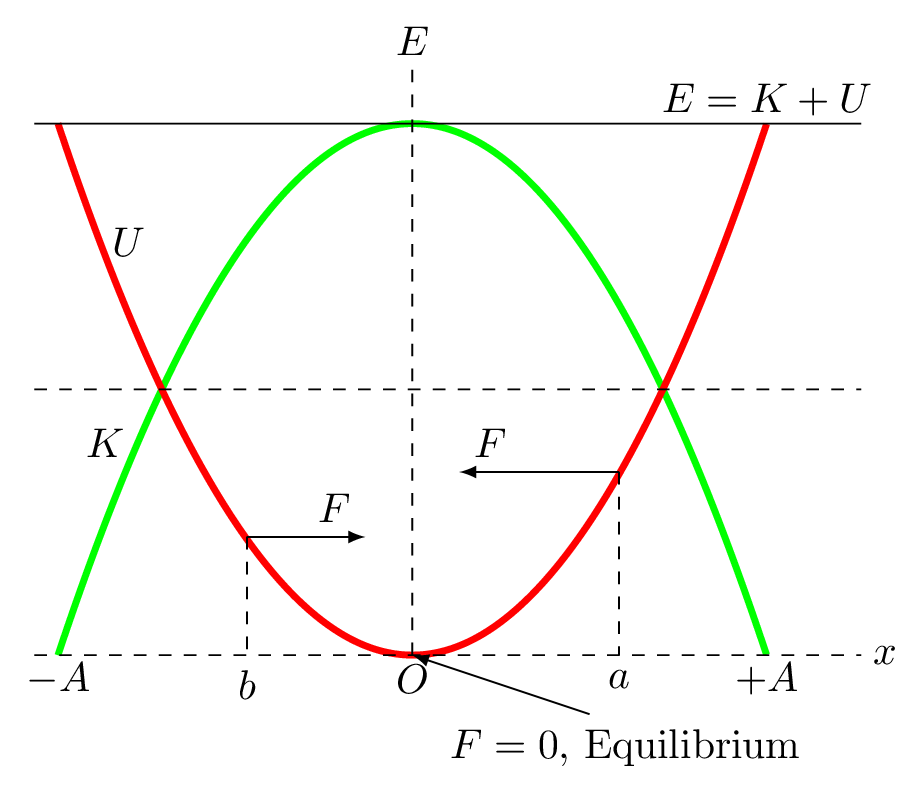
From the principle of conservation of energy as kinetic energy of the system increases its potential energy decreases. This means the force acting on a particle is the rate at which the potential energy decreases in any given direction as shown in Figure 5.1.4.(a). At point a, the slope of \(U(x)\) is positive, i.e., the x-component of the force is in the negative x direction. At the point b, the slope is negative and hence the force is positive. The force increases as the slope of \(U(x)\) increases. The point in the middle, at \(x = 0\text{,}\) is is a minimum of \(U(x)\) and hence the slope is zero. Therefore the x-directed force F at that point is zero as well. A point at which the force on an object is zero is a point of static equilibrium [Subsubsection 4.1.4.1], i.e., a particle is at rest and will remain there at rest. If the particle is displaced by a small distance to the right or the left of the equilibrium point, the force pushes the particle back towards equilibrium. Points where the force is zero and small displacements cause a restoring force to bring the particle back to the same points are called stable equilibrium points [Subsection 4.11.2].
Remember force is a negative gradient of the potential energy, i.e.,
\begin{equation*}
\vec{F}= -\frac{\,dU}{\,dr} \qquad [\because U(r) = W= -\vec{F}\cdot\,dr]
\end{equation*}
\begin{equation*}
\text{or,}\quad \vec{F_{x}}= -\frac{\,dU}{\,dx};
\end{equation*}
\begin{equation*}
\vec{F_{y}}= -\frac{\,dU}{\,dy};
\end{equation*}
\begin{equation*}
\text{and}\quad\vec{F_{z}}= -\frac{\,dU}{\,dz}
\end{equation*}
That is, the force is a negative slope of the potential energy function in its direction. If a particle moves in the direction of the (conservative) force, it speeds up and its kinetic energy increases.
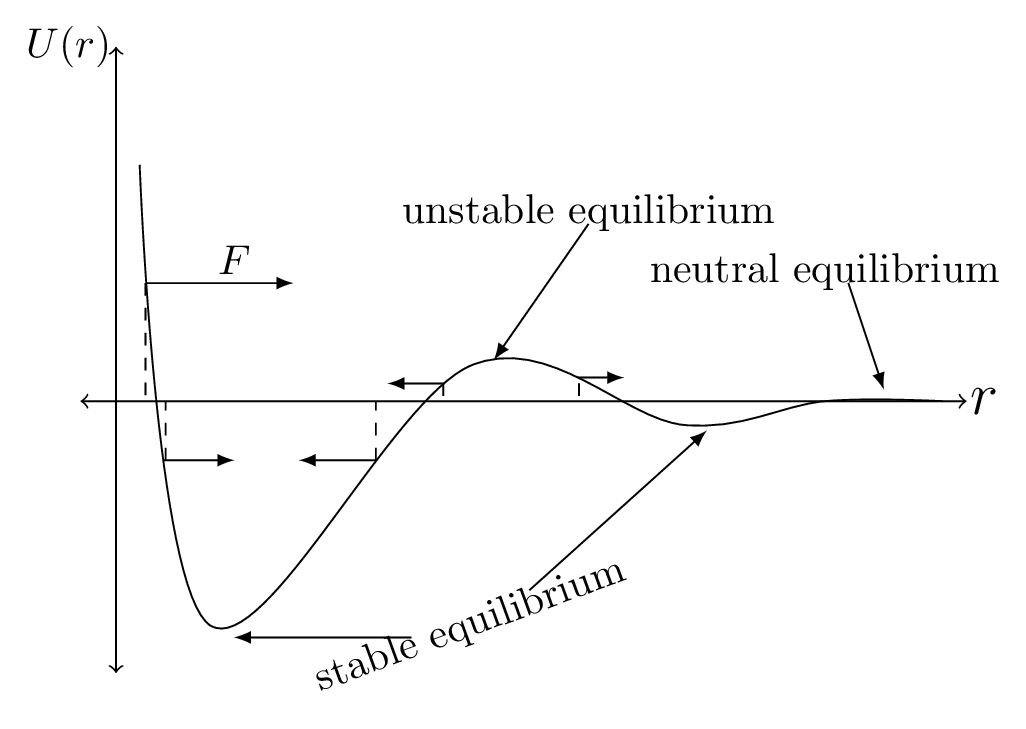
The forces between neutral atoms are extremely small, nearly zero, if atoms are very far away from one another. This is illustrated as an extended region where the potential energy is flat for large r as shown in Figure 5.1.4.(b). Such region is called neutral equilibrium [Subsection 4.11.2] because there are no forces that either restore or repel the two atoms. When two atoms reaches closer, their interaction becomes first weakly attractive due to quantum dipole-induced dipole interactions and then weakly repulsive as the two atoms start to touch each other. There is a potential energy minimum in between where two atoms separated by a certain distance can be in stable equilibrium without being chemically bound. If atoms approaches more closely then they encounter a second potential energy well that is at first strongly attractive to an actual chemical interaction between them followed by a hard core repulsion as the electron clouds are prevented from interpenetrating by the Pauli exclusion principle. This second potential energy well is often modeled by a Lenard-Jones potential energy corresponding to the inverse powers of \(r\text{.}\) It also has a point of stable equilibrium. In between, there is a point where the growing attraction of the inner potential energy well and the growing repulsion of the outer potential energy well balance, so that the potential energy function has a maximum. At this maximum the slope is zero, a position of force equilibrium but because the force on either side of this point pushes the particle away from it, this is a point of unstable equilibrium [Subsection 4.11.2]. Unstable equilibria occur at isolated maxima in the potential energy function, just as stable equilibria occur at isolated minima.
4
Introductory Physics-I, Robert Brown, Duke University
