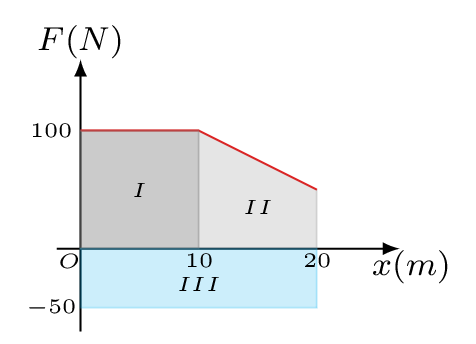
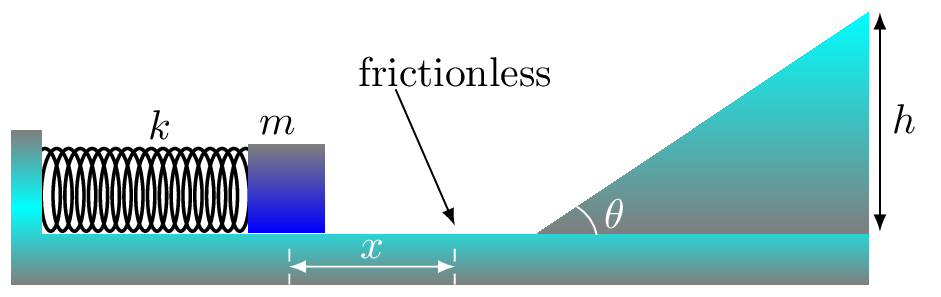
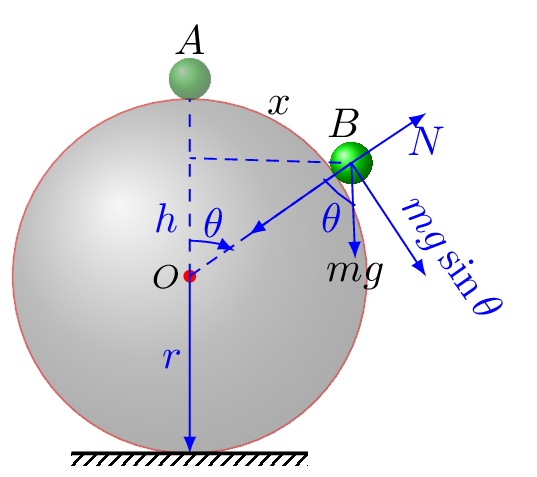
Given: \(r=1m, f=0,\quad x=?\text{.}\)
Suppose the ball of mass \(m\) is sliding down the sphere on a circular track. The necessary centripetal force \(F_{c}\) is then provided by the radial component of its weight and the normal force.
\begin{equation*}
mg\cos\theta -N = \frac{mv^{2}}{r}
\end{equation*}
At the point where the ball leaves the sphere normal force must be zero, i.e.,
\begin{equation*}
N=0.
\end{equation*}
\begin{equation*}
\therefore mg\cos\theta = \frac{mv^{2}}{r};
\end{equation*}
\begin{equation*}
\text{or,} \hspace{3pt} \cos\theta = \frac{v^{2}}{rg}
\end{equation*}
\begin{equation}
\text{or,}\quad v^{2} =rg\cos\theta \tag{5.3.6}
\end{equation}
From the principle of conservation of energy, we have -
\begin{equation*}
PE_{A}+KE_{A}=PE_{B}+KE_{B}
\end{equation*}
Assume B is a point where ball leaves the sphere.
\begin{equation*}
mg(2r) +0 = mg(h+r)+\frac{1}{2}mv^{2}
\end{equation*}
\begin{equation*}
\text{or,} \quad 2gr = g(r\cos\theta+r) +\frac{v^{2}}{r} \quad [\because h=OB\cos\theta =r\cos\theta]
\end{equation*}
\begin{equation*}
\text{or,} \quad 2gr-gr(1+\cos\theta)=\frac{1}{2}(gr\cos\theta)
\end{equation*}
\begin{equation*}
text{or,} \quad 1-\cos\theta =\frac{\cos\theta }{2}
\end{equation*}
\begin{equation*}
\text{or,} \quad 1=\frac{3}{2}\cos\theta
\end{equation*}
\begin{equation*}
\theta = \cos^{-1}\left(\frac{2}{3}\right)=48^{o}
\end{equation*}
\begin{equation*}
\therefore x=r\theta = 1m\times \frac{\pi}{180}\times 48^{o} =0.84 \,m
\end{equation*}
[using radian formula]
\begin{equation*}
\text{or,}\quad y = 2r-(h+r) = r-h = r-r\cos\theta = r\left(1-\frac{2}{3}\right) = \frac{1}{3}r
\end{equation*}
where \(x\) and \(y\) are the distance on the surface of sphere and depth below point \(A\) at which the ball left the sphere.