Subsection 5.1.3 Conservative and Non-Conservative Forces
If a body under the action of a force does no net work during any closed loop, then the force is conservative, otherwise, it is non-conservative. Non-conservative forces are dissipative forces such as friction or air resistance. These forces take energy away from the system as the system progresses, energy that you can’t get back. These forces are path dependent and therefore it matters where the object starts and stops. Gravity, spring force, electric and magnetic, and other restoring forces are conservative. Friction, normal force, tension, and other applied forces are non-conservative. Conservative forces are state function, and non-conservatives forces are path function. The work done by a conservative force is independent of the path, i.e., the work done by a conservative force is the same for any path connecting two points.
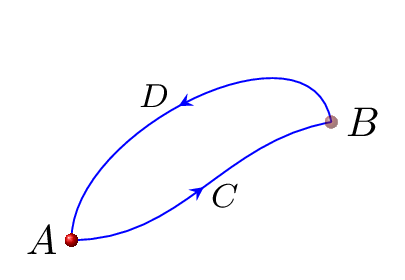
\begin{equation*}
W_{ACB} = \int\limits_{AB}\vec{F}\cdot\,d\vec{r}=W_{BDA} =\int\limits_{BA}\vec{F}\cdot\,d\vec{r}
\end{equation*}
\begin{equation*}
\therefore W_{ABA} = \oint \vec{F}\cdot\,d\vec{r} =0\quad [\because W_{BDA}=-W_{ACB}]
\end{equation*}
Mathematically, the work done is independent of path if the infinitesimal work \(\vec{F}\cdot\,d\vec{r}\) is an exact differential. In two dimensions, the condition for
\begin{equation*}
\vec{F}\cdot\,d\vec{r} = F_{x}\,dx+ F_{y}\,dy
\end{equation*}
to be an exact differential is
\begin{equation*}
\frac{\,dF_{x}}{\,dy}=\frac{\,dF_{y}}{\,dx}.
\end{equation*}
The work done by a non-conservative force depends on the path taken, i.e., \(\frac{\,dF_{x}}{\,dy}\neq\frac{\,dF_{y}}{\,dx}.\)
